Exercice en complément du cours

Exercice : Largeur de raie pour un gaz à température ambiante
Dans leur référentiel, les atomes émettent selon une forme de raie f(u) décrite par :
f( )1
2
0
 2
La probabilité de trouver un atome de vitesse comprise entre v et v+dv s'écrit P(v)
dv. Avec :
P( v ) 1
2
1
D
expv2
2
D
2
avec :
D
2kBT
M
M masse atomique et kB=1,38 10-23JK-1.
On suppose :
0 D
c
.
Donner la forme et la largeur de raie observée sur un détecteur dans le référentiel du
laboratoire.
--------------------------------------------------------
La fréquence u0 émise par un atome de vitesse v est vue sur le détecteur à la
fréquence
0 01v
c
.
La forme de raie associée est
fv( )1
2
01v
c
. La fome de raie
totale correspond à la moyenne :
f( )fv()
 P(v) dv
En posant
x
0
cv
, on obtient :
f( ) 1
2
0x
 21
2
1
D
exp
c
0
x
2
2
D
2
c
0
dx

f(u) a un profil appelé profil de Voigt. La demi-largeur à mi-hauteur de la partie
lorentzienne de l'intégrale est G. La demi-largeur à mi-hauteur de la partie gaussienne
est
2 n2
D
0
c
.
Comme
D
0
c
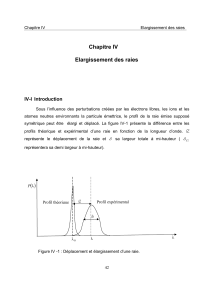
, la forme relative des deux fonctions est la suivante :
La gaussienne a donc une valeur constante, là où la lorentzienne est non nulle.
D'où:
f( )1
2
1
D
c
0exp
c
0
0
2
2
D
2
1
2
0x
 2dx.
La valeur de l'intégrale est 1 car la fonction f(n) est normalisée
f( )1
2
1
D
c
0exp1
2c2
0
2
D
2
0
 2
f(u) a un profil gaussien de demi-largeur totale à mi-hauteur :
2 2 n2
D
0
c
AN : raie verte de mercure à T = 300 K.
l = 546 nm, M = 200 x 1,66 10-27 kg
-> Dn = 0,5 GHz.