Filtrage linéaire (Ex)

PCSI 2 Filtrage linéaire
2016 – 2017 1/8
FILTRAGE LINEAIRE
I Filtre de Wien
On alimente le circuit de Wien représenté ci-contre par une tension alternative
€
ve(t)
d'amplitude constante et de pulsation variable. On introduit le paramètre fréquentiel sans
dimension .
1) Nature du filtre
a) Faire un équivalent du montage en basse fréquence puis en haute fréquence et
déterminer
€
vs(t)
dans les deux cas.
b) En déduire la nature probable du filtre.
2) Fonction de transfert
a) La fonction de transfert du circuit peut se mettre sous la forme :
€
H(jx)=1
3+j x −1
x
⎛
⎝
⎜ ⎞
⎠
⎟
.
De quel type de filtre s’agit-il ? Justifier.
b) Pour quelle fréquence
€
f1
(en fonction de R et C), les tensions et sont-elles en phase ? AN.
3) La tension d'entrée est désormais une tension triangulaire (figure ci-dessous) de pulsation
€
ω
0
et de période
€
T0=2
π
ω
0
=3
f1
, dont
l’expression s'écrit sous la forme approchée :
€
ve(t)=8Em
π
2cos
ω
0t+1
32cos 3
ω
0t+1
52cos 5
ω
0t+...
⎛
⎝
⎜ ⎞
⎠
⎟
.
Si l’on suppose que la bande passante du filtre est très étroite :
a) Quelle sera la forme du signal de sortie ?
b) Quelle sera sa fréquence ? Que vaut
€
f0
?
c) Quelle sera son amplitude ?
Données numériques : R = 20 kΩ ; C = 50 nF ; Em = 1,0 V.
Réponse : passe-bande ; f1 = 1,6.102 Hz ; f0 = 53 Hz ; Vsm = 30 mV.
II Un gain particulier !
Un quadripôle du premier ordre possède la fonction de transfert :
€
H(jx)=1−jx
1+jx
, où x = RCω est la pulsation réduite.
1) Déterminer le gain G(x) et le déphasage ϕ(x).
Commenter : quel pourrait être l’utilisation d’un tel dispositif ?
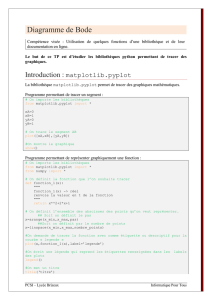
2) Le logiciel Scilab fournit le diagramme de Bode ci-contre.
Commenter.
3) On prend R = 1,0 kΩ et C = 0,1 nF. On applique un signal
€
ve(t)=Vem cos ω t
avec Vem = 1,0 V et ω = 1,0.105 rad.s-1.
Déterminer le signal de sortie
€
vs(t)
.
4) Même question pour C = 10 nF et 1 µF, les autres valeurs
étant inchangées.
€
ω
€
x=RC ω

PCSI 2 Filtrage linéaire
2016 – 2017 2/8
Réponse : G(x) = 1 et j(x) = - 2 arctan x ;
€
vs(t)≈ve(t)
) puis
€
vs(t)≈1,0sin ω t
puis
€
vs(t)≈ −ve(t)
.
III Mise en cascade de filtres
Pour toutes les questions, on pose
€
ω
o=1
RC
et
€
x=
ω
ω
o
.
L’AO est idéal et fonctionne en régime linéaire.
1) On considère le circuit de la figure 1.
Calculer la fonction de transfert
€
H1jx
( )
=s
e
de ce filtre.
On donne la courbe de gain du diagramme de Bode en fin d’énoncé (courbe
H1). De quel type de filtre s’agit-il ?
2) On considère le circuit de la figure 2. La fonction de transfert s’écrit
€
H2jx
( )
=v
e=1
1+3jx −x2
.
On donne la courbe de gain du diagramme de Bode en fin d’énoncé (courbe H2).
De quel type de filtre s’agit-il ? Comparer au filtre précédent.
3) On considère le circuit de la figure 3. Quel est le rôle du suiveur ? La fonction de transfert s’écrit
€
H3jx
( )
=w
e=1
1+2jx −x2
.
On donne la courbe de gain du diagramme de Bode en fin d’énoncé (courbe H3).
De quel type de filtre s’agit-il ? Comparer aux filtres précédents.
Réponse :
€
H1jx
( )
=1
1+jx
passe-bas d’ordre 1 ; les deux autres sont passe-bas d’ordre 2 avec des coupures différentes.
IV Circuit RLC série
Le circuit RLC série suivant est réalisé avec un condensateur de capacité C = 240 nF, un résistor de résistance R = 25 Ω et une bobine
inconnue d’inductance L et de résistance de bobinage RL. On note ub(t) la tension aux bornes de cette bobine (voir figure ci-dessous).
Ce circuit est alimenté par un GBF de f.e.m. e(t) = em cos (ωt). En notation complexe, la fonction de transfert de ce filtre est H = ub/e.
1) En justifiant, déterminer rapidement la nature de ce filtre.
2) Lorsque la pulsation du générateur est égale à la pulsation propre ωo = (LC)-1/2, quelle est la valeur du module de H ?
3) L’amplitude la tension uR passe par un maximum lorsque la fréquence f = 1050 Hz. En déduire la valeur de L.
R
s(t)
e(t)
C
Figure 1
R
e(t)
C
Figure 2
R
v(t)
C
R
e(t)
C
Figure 3
R
w(t)
C
suiveur

PCSI 2 Filtrage linéaire
2016 – 2017 3/8
4) On observe sur un oscilloscope (voir figure ci-dessus) les tensions e(t) et uR(t) à une fréquence f1 supérieure à 1050 Hz. Une
demi-période du signal du générateur occupe 9 carreaux de l’axe horizontal. Le calibre vertical est le même sur les deux voies : 1
carreau = 2V. Quel est le déphasage φ de uR par rapport à e ?
5) Déduire de φ la valeur de RL.
6) Sachant que f1 = 1080 Hz, déterminer la valeur du facteur de qualité Q de ce circuit.
Réponse : passe-haut ;
€
H=
RL
2+L2
ω
o
2
R+RL
; L = 96 mH ; φ = - 45 ° ; RL = 10 Ω ; Q = 18.
V Etude de la suspension d’un véhicule
Dans le cadre d’un modèle simplifié de suspension, on
assimile le véhicule à un point matériel M de masse m posé
sur un ressort dont l’autre extrémité S peut se déplacer le
long d’une route horizontale ou bosselée.
Le ressort a une constante de raideur k et une longueur à
vide L0.
On repère les positions respectives de M et de S par leurs
cotes z et z1 sur un axe vertical Oz ascendant tel que z1 = 0
lorsque S se déplace sur la route horizontale.
En outre, le point matériel M est soumis à l’action d’un
amortisseur fluide, de coefficient d’amortissement α
(positif), disposé entre les points M et S. Le point matériel
subit alors de la part de cet amortisseur une force de
frottement de la forme :
€
!
F
frott =−
α v−v1
( )
!
u
z
, en notant
€
v=˙ z
et
€
v1=˙ z
1
les vitesses respectives de M et S lors de
leurs déplacements verticaux,
€
!
u
z
étant les vecteur unitaire
ascendant de l’axe Oz.
Le coefficient α peut être réglé par la variation du débit
d’huile à travers un trou percé dans le piston mobile de
l’amortisseur.
Le véhicule se déplace d’abord sur une route parfaitement horizontale (z1 = 0). La cote de M est constante, de valeur ze, dans ce régime
dit stabilisé.
1) Déterminer ze en fonction de m, g (accélération de la pesanteur), k et L0. On détaillera soigneusement les étapes de ce calcul.
Le véhicule se déplace à présent sur une route bosselée. On note Z(t) = z(t) – ze l’écart à la position d’équilibre à l’instant t.
2) Montrer que Z(t) vérifie une équation différentielle de la forme :
€
md2Z(t)
dt 2+
α
dZ (t)
dt +kZ (t)=F(t)
,
F(t) étant une fonction de
€
x1(t)
, de
€
˙
x
1(t)
, et des constantes α et k que l’on précisera. Commenter la signification de F(t).
Le profil de la route « en tôle ondulée » est tel que F(t) est une fonction sinusoïdale du temps de pulsation ω.
ez
z
α
k, Lo
M (m)
Route horizontale
O
z
z1
Route bosselée
S
e(t)
uR(t)

PCSI 2 Filtrage linéaire
2016 – 2017 4/8
En régime sinusoïdal forcé et en notation complexe, le comportement du véhicule est décrit par la fonction de transfert :
€
H=Z
z1
.
On note
€
ω
0=k
m
la pulsation propre du véhicule,
€
Q=km
α
son facteur de qualité et
€
x=
ω
ω
0
la pulsation réduite.
3) Etablir l’expression de la fonction de transfert et la mettre sous forme canonique
€
Hjx
( )
en fonction de x et de Q.
On donne ci-dessous le diagramme de Bode en amplitude
€
HdB (log x)
pour Q = 2,5.
4) En s’appuyant sur ce graphe, répondre aux questions suivantes (elles ne demandent tout au plus qu’une réponse qualitative mais
justifiée, ou quantitative s’appuyant sur quelques lignes de calcul) :
a) Que se passe-t-il si le ressort du système est très
raide (constante de raideur élevée) ?
Est-ce confortable pour les passagers ?
b) Quel phénomène se produit-il vers x = 1 ?
Est-ce confortable pour les passagers ?
A quel vitesse du véhicule en km.h-1 cela
correspond-il si m = 0,5.103 kg, k = 50.103 N.m-1,
et si les bosses sont régulièrement espacées d’une
distance λ = 1 m.
c) Dans le film « Le salaire de la peur » de Henri-Georges Clouzot (1953), Yves Montand conduit un camion chargé de
nitroglycérine. Il passe sur un tronçon de route en tôle ondulée. Afin d’éviter l’explosion du chargement, il décide
paradoxalement de traverser cette partie du trajet à une vitesse élevée.
Justifier qualitativement cette attitude à l’aide des résultats précédents.
Plus précisément, la vitesse du camion étant telle que la fréquence de sollicitation est de 8,0 Hz (et la fréquence propre du
véhicule restant la même qu’à la question précédente), quelle sera l'amplitude des oscillations de la caisse du camion si les
bosses ont une hauteur de 10 cm ?
La force excitatrice F(t) sinusoïdale de pulsation ω et d’amplitude Fm est notée
€
F(t)=Fmcos ω t
( )
.
5) Déterminer l’amplitude Vm de la vitesse d’oscillation verticale du véhicule en fonction de Fm, m, k, α et ω.
Pour quelle pulsation ω est-elle maximale ?
Réponse :
€
z0=l0−mg
k
;
€
F=kz1+ α
˙
z
1
;
€
Hjx
( )
=
1+jx
Q
1−x2+jx
Q
; inconfortable car le véhicule reproduit le profil de la route ; résonance
donc inconfortable ; v = 5,7 km.h-1 ; Zm = 5,0 mm ;
€
Vm=Fm
α +j m ω −k
ω
⎛
⎝
⎜ ⎞
⎠
⎟
maximale pour ω = ω0.
VI Réalisation d'un atténuateur d'oscilloscope
Un oscilloscope ne permet de visualiser une tension qu’en deçà d’une valeur recommandée par le fabriquant. Au-delà de cette limite,
on envoie le signal à mesurer par l'intermédiaire d'une sonde réductrice de tension (atténuateur) qui applique à l'entrée de l'appareil une
fraction "α" de la tension. On cherche ici à déterminer l’architecture et les grandeurs caractéristiques de cette sonde.
Partie A : préliminaires (cours)
1) Valeur efficace
a) Proposer en une phrase une définition de la valeur efficace I de l’intensité i(t) d’un courant périodique de forme quelconque.
b) En déduire une expression mathématique de celle ci sous la forme d’une intégrale pour une intensité T-périodique.
c) On considère un signal sinusoïdal de la forme u1(t) = U1m cos ωt, d’amplitude U1m et de pulsation ω. Déduire de la question

PCSI 2 Filtrage linéaire
2016 – 2017 5/8
précédente sa valeur efficace U1 (dite « rms ») en fonction de son amplitude.
d) On donne en annexe un extrait de la notice de l’appareil « RIGOL DS2000 » utilisé en TP. La tension maximale d’entrée
dépend de la classe de sécurité de l’installation sur laquelle se fait la mesure. Donner la valeur numérique de l’amplitude
maximale admissible en catégorie I (c’est-à-dire pour des mesures effectuées sur un dispositif possédant une liaison à la terre
des carcasses métalliques des appareils).
2) Diviseur idéal de tension
On considère un diviseur idéal de tension en régime sinusoïdal forcé, et en notation complexe, formé par la mise en série de
deux impédances Z1 et Z2 (figure 1).
Figure 1
Etablir la formule du diviseur idéal de tension donnant la tension U2 aux bornes de Z2 en fonction de Z1, Z2 et de la tension
totale U aux bornes de la totalité du diviseur.
3) Association de deux dipôles en régime sinusoïdal forcé
Comment s’associent les admittances (inverses d’impédances) en dérivation ? En faire la démonstration.
En déduire l’admittance de l’association en dérivation d’un résistor de résistance R et d’un condensateur de capacité C.
Partie B : première tentative …
Cahier des charges de la sonde : si on appelle U1 la tension à mesurer, on voudrait obtenir à l'entrée de l'oscilloscope, après
l'atténuateur, une tension U2 telle que :
€
U2
U1
= α
(figure 2).
Figure 2 Figure 3
L'oscilloscope, vu de ses bornes d'entrée, se ramène à une impédance constituée par une résistance R et un condensateur C en parallèle.
Dans un premier temps, on réalise un atténuateur constitué d’un simple résistor de résistance Ra (figure 3).
1) Montrer que la fonction de transfert complexe
€
H j ω
( )
=U2
U1
s'écrit :
€
H j ω
( )
=
α
1+j
ω
ω
0
(on pourra utiliser la formule du diviseur
idéal de tension).
Exprimer α et ω0 en fonction de Ra, R et C.
2) On donne l'allure du diagramme de Bode de l’atténuateur pour α = 0,1 et .
€
x=
ω
ω
0
Atténuateur
(sonde)
Oscilloscope
U1
U2
Oscilloscope
Atténuateur
U2
U1
Ra
R
C
€
U2
€
U
€
Z2
€
Z1