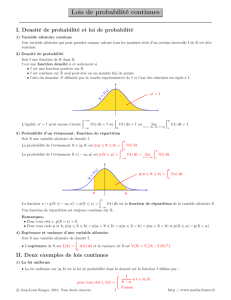
I. Lois de probabilité à densité 1. Variable aléatoire à densité Dans

Chapitre XI : Lois continues
Extrait du programme :
I. Lois de probabilité à densité
1. Variable aléatoire à densité
Dans de nombreux domaines, on est amené à étudier des variables aléatoires pouvant prendre, du
moins théoriquement, toute valeur d’un intervalle I de .
Ces variables aléatoires sont dites continues.

Exemple : On veut définir la variable aléatoire X qui, a tout téléviseur, associe sa
durée de bon fonctionnement exprimée en heures.
Cette durée peut prendre toute valeur de l’intervalle I = [0 ; 50000]. On va alors
chercher à calculer des probabilités de la forme P X    ou P X   .
Pour cela, on utilise une fonction f définie sur I, donc cf est la courbe représentative
dans un repère orthogonal : la probabilité Pa  X b est définie comme l’aire
(exprimée en unités d’aire) du domaine compris entre l’axe des abscisses, la courbe
cf et les droites d’équations xa et xb.
Définitions :
On appelle fonction de densité de probabilité sur l’intervalle I, toute fonction f définie, continue et
positive sur I telle que l’intégrale de f sur I soit égale à 1.
Une variable aléatoire à densité X sur un intervalle I est définie par la donnée d’une fonction de
densité de probabilité f définie sur I. La probabilité pour que X appartienne à un intervalle [a ;b] de I
est égale à l’aire sous la courbe de f sur [a ;b].
Pa  X  b  
a
b ftdt
On en déduit que le domaine compris entre la courbe représentative de f et l’axe des abscisses a pour
aire P(XI) c’est-à-dire 1.
Propriétés : Pour tous réels a et b appartenant à l’intervalle I :
(1) PXa)  
a
a ftdt=0
(2) Pa  X  b  P a  X  b  Pa  X  b P a  X b
2. Espérance mathématique
Définition : Soit X une variable aléatoire continue de fonction densité f sur l’intervalle [a ;b], alors
l’espérance mathématique de X est le réel défini par :
EX = 
a
b tftdt
Point méthode 61 : Utiliser une loi à densité
La production quotidienne X d’un produit en tonnes est une variable aléatoire continue qui
prend ses valeurs dans l’intervalle [0 ;10] avec la densité de probabilité f définie par :
fx  ,  x  x
1. Vérifier que f est bien une densité de probabilité sur [0 ;10]
2. a. Calculer les probabilités des événements A : « X 7 » et B : « la production quotidienne
dépasse 6 tonnes ».
b. Calculer PB(A) à 0,001 près.
Solution :
1. pour vérifier si une fonction est une densité de proba sur un intervalle, il faut vérifier :
- Que f est bien continue et positive sur I
- Que l’intégrale de f sur [0 ;10] vaut bien 1
f est une fonction polynôme du second degré, donc f est continue sur [0 ;10].

Pour tout réel x, fx  ,  x  x  ,x  x  ,x  ,x
Donc les racines de f sont 0 et 10.
Par conséquent, f est positive entre les racines (car a=  0,006 négatif), soit f positive sur [0 ;10].
De plus,
 ,xx²dx = 0,006   xx²dx = 0,006   
= 0,006 
 0 =1
f est donc continue, positive sur [0 ;10] et 
 ftdt = 1 c’est donc bien une fonction densité.
2. a. P(A)= P (X 7) = 
 fxdx = F(7 F(0)=0,006 
 – 
 = 0,784
P(B)= P (X > 6) = 1 P(X  6) = 1 
 fxdx = 1 ( )
FF
= 10,006 ( )   = 0,352
b. PB(A) = PBA
PB = PX et X  PB = P X   PX  =  ,
 fxdx = , – ,
,
0,386
II. Loi uniforme sur [a ;b]
1. Définition et propriétés
Définition : a et b désignent deux nombres réels distincts.
Dire qu’une variable aléatoire X suit une loi uniforme sur l’intervalle [a ;b] signifie que la densité de
probabilité de la loi X est une fonction constante sur [a ;b].
Propriété : la densité de probabilité de la loi uniforme sur [a ;b] est la fonction f définie sur [a ;b] par :
fx  
b  a
Démonstration : On sait que l’aire sous la courbe entre a et b soit être égale à 1
donc : si fx  k on a :
kb  a   donc k  
b  a
CQFD
Propriété : X est une variable aléatoire qui suit la loi uniforme sur [a ;b].
Pour tout intervalle [c ;d] inclus dans [a ;b] on a : P(c  X  d ) = d  c
b  a
Démonstration : P(c  X  d) = 
c
d fxdx = 
c
d 
badx =  ba 
c
d dx = 
ba [ ]
xd
c = dc
ba CQFD
Remarques :
 Par convention, choisir un nombre au hasard dans un intervalle [a ;b] c’est le choisir selon la
loi uniforme sur l’intervalle [a ;b].
 En particulier, pour la loi uniforme sur [0 ;1] et pour tous nombres réels c et d de [0 ;1] :
P(c  X d) = dc
 = dc

Donc la probabilité de choisir un nombre au hasard entre c et d est égale à la longueur de
[c ;d].
2. Espérance
Propriété : X est une variable aléatoire qui suit la loi uniforme sur [a ;b].
Son espérance est : EX)= ab
Démonstration : On sait que l’espérance d’une variable aléatoire X de densité f sur [a ;b] est donnée
par : EX = 
a
b tftdt
Or ici, X suit une loi uniforme donc fx  
b  a
Ainsi, E(X)= 
ba 
a
b tdt = 
ba   t²b
a = 
b  a b   a   b  a( )
b  a  b  ab  a
b  a  b  a
CQFD
Point méthode 62 : Calcule une probabilité avec une loi uniforme
Caroline a dit qu’elle passait voir Julien à un moment quelconque entre 18h30 et 20h45. Quelle est la
probabilité qu’elle arrive pendant le feuilleton préféré de Julien qui dure de 19h à 19h30 ?
Solution : Choisir l’heure d’arrivée de Caroline, c’est choisir un nombre au hasard dans [18,5 ; 20,75].
Par convention, la loi de X est la loi uniforme sur cet intervalle.
X est la variable aléatoire égale à l’heure d’arrivée de Caroline chez Julien. Elle prend ses valeurs dans
l’intervalle [18,5 ;20,75].
X suit une loi uniforme sur [18,5 ; 20,75] donc :
P(19  X  19,5) = ,
,, = , , = 
La probabilité que Caroline arrive pendant le feuilleton est de 
.
III. Loi exponentielle de paramètre 
Contexte et modèle : La durée de vie d’un appareil (comme un
composant électronique) est une variable aléatoire X prenant ses valeurs
dans [ 0, +[. Si l’on suppose que cette durée de vie ne dépend pas du
temps pendant lequel l’appareil a déjà fonctionné (on dit que la durée
de vie est sans vieillissement).
X suit alors une loi exponentielle.
Définition : Soit  un réel strictement positif.
Une variable aléatoire X suit la loi exponentielle de paramètre  si sa densité de probabilité est la
fonction f définie sur [0 ;+[ par : f ( t ) = 
  et si t  0
 si t < 0
On dit que X~ e()

Propriété :
Si X suit la loi exponentielle de paramètre , alors pour tous réels a et b tels que 0  a  b :
P ( a X b ) = e −
a − e − b
En particulier : P ( X b ) = 1 − e − b
P ( X > a ) = e − a
Démonstration : La fonction x  e − x est une primitive de f sur [0 ;+[
On en déduit que P ( a X b ) = 
a
b  e − x dx = [ e −
x ]b
a = e − b − ( e − a )
= e − a − e − b
En particulier : P ( X b ) = P ( 0 X b ) = 1 − e − b
Et donc : P ( X > a ) = 1 − P ( X a ) = e − a
CQFD
Définition : L’espérance mathématique d’une variable aléatoire X suivant une loi de paramètre  est
définie par : E ( X ) = lim
b  +
0
b xf ( x ) dx avec f ( x ) =  e − x .
Propriété :
E ( X ) = 1
Démonstration : (BAC)
Soit g la fonction définie sur [0 ;+[ par : g ( x ) = xf ( x ) = x e − x
On cherche une primitive G de g de la forme G ( x ) = ( Ax + B ) e −
x avec A et B réels.
Pour tout nombre réel positif x : G’ ( x ) = A e − x + ( Ax + B ) ( −  e − x )
= ( −  Ax + A −  B ) e −
x
G est une primitive de g sur [0 ;+[ si et seulement si G’ ( x ) = g ( x ) pour tout réel positif x, c’est-à-
dire : ( −  Ax + A −  B ) e −
x = x e − x
Pour que cette égalité soit vrai, on doit donc avoir :
 −  A = 
A −  B = 0  
 A = − 1
B = − 1
 d’où G ( x ) = 
− x − 1
 e − x .
Alors pour tout réel positif b : 
0
b xf ( x ) dx = G ( b ) − G ( 0 )
=  − b − 1
 e − b + 1
= 1
 ( −  be − b − e − b + 1 )
lim
b  +
−  b = − et lim
X  −
Xe X = 0 donc lim
b  +
−  be − b = 0
lim
b  +
−  b = − et lim
X  −
e X = 0 donc lim
b  +
e − b = 0
D’où lim
b  +
( −  b e −
b − e − b + 1 ) = 1
Et ainsi, lim
b  +
0
b xf ( x ) dx = 1
, soit E ( X ) = 1  CQFD