Électronique numérique : logique séquentielle

Un livre de Wikibooks.
Contenu transféré sur Wikiversité
Le contenu que vous recherchez a été déplacé vers la Wikiversité. Il
devrait être disponible sous le nom Logique séquentielle.
Livre à fractionner
Il a été suggéré de fractionner ce livre en plusieurs sous-pages afin d'améliorer sa
lisibilité.
TD1 : mémoires et bascules
Mémoires RS
La mémoire est un composant permettant de retenir de l'information. C'est un élément qui ne peut pas être réalisé en
combinatoire pur. Pour son étude il faut donc des méthodes différentes que les tables de vérité. On utilisera une table
d'évolution qui ressemble à une table de vérité. La différence est qu'il apparaît dans cette table la sortie au présent (notée
q) et la sortie au futur (notée Q).
Table d'évolution
Entrées Etat futur Fonction réalisée
RS Q ou Q +
0 0 q mémorisation
0 1 1 mise à un
1 0 0 mise à zéro
1 1 X priorité(ou interdite)
L'entrée S sert donc à mettre à 1, tandis que R sert à mettre à 0. La dernière ligne de la table d'évolution n'est pas traitée
p
ar tous de la même manière. On trouve souvent dans la littérat
u
re une interdiction concernant cette ligne : elle est en
général liée au fait que les sorties souhaitées sont alors au nombre de deux et notées Q et Nous choisissons plutôt
d'étudier une seule sortie notée Q et ainsi d'autoriser cette ligne. Il se trouve un X dans cette ligne parceque l'on considère
qu'il peut y avoir trois cas :
0 on parle de mémoire à Reset prioritaire,
1 on parle de mémoire à Set prioritaire,
q on parle alors de mémoire à mémoire prioritaire.
Exemple
N
ous proposons le schéma suivant et son tableau de Karnaugh associé :

Remarquez la variable q introduite dans le tableau de Karnaugh (alors que le circuit n'a en réalité que deux entrées). Ce
tableau de Karnaugh sert à déduire une équation de récurrence. On qualifie ces équations de récurrence car une variable
intervient à la fois comme entrée et comme sortie (évidemment ici q et Q : qui ne sont reliées que par un fil).
L'équation de récurrence s'écrit :
Exercice 1
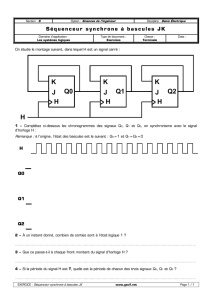
Pour le schéma ci-dessous, compléter le tableau de Karnaugh ainsi que le diagramme des temps. On supposera pour
simplifier que les portes répondent de manière instantanée (ce que l'on a toujours fait jusqu'à maintenant).
Mémoire D (D latch)
Cette fonction comporte deux entrées D et H et une sortie Q. L'équation de récurrence de la mémoire D n'a pas beaucoup
d'intérêt, il vaut mieux retenir son fonctionnement : recopie son entrée D sur sa sortie Q lorsque son horloge H est à 1.
Bascule D
Cette fonction comporte aussi deux entrées, D et H et une sortie Q. La grande différence est que la recopie de l'entrée sur
la sortie ne se fait maintenant que sur front d'horloge. Notez sur le schéma ci-dessous comment est notée cette sensibilité
au front d'horloge.
La bascule D la plus complexe comporte quatre entrées D, H, S et R et une sortie Q. Les entrées supplémentaires sont
actives à l'état bas (donc notées parfois /S et /R) et ont les même fonctions que dans le cas d'une mémoire. Elles sont dites
asynchrones dans le sens où contrairement à D elles sont complètement indépendantes des fronts d'horloge.

Plus d'information ici : Bascules.
Bascules JK
Vous trouverez ici (Wiki : Bascules) des informations sur la bascule JK.
N
ous complèterons cette information avec ce que l'on appellera
d
ans la suite un diagramme d'évolution. Ici il est
constitué de deux états (en vert) et de transitions (les flèches). Ce diagramme d'évolution est très important pour nous car
il nous servira lors des synthèses.
Exercice 2
Transformer une bascule JK en bascule D. Transformer ensuite une bascule D en bascule JK.
Exercice 3
N
ous désirons réaliser la bascule E suivante.
si E=0 alors Q=1
si E=1 alors Q(n+1) = /Q(n).
TD2 : Diagrammes d'évolution, équations de récurrence
Diagrammes d'évolutions
Les montages séquentiels simples sont en général représenté par un diagramme d'évolution. Il s'agit d'un ensemble d'états
(cercles) reliés entre eux par des flèches (transitions).
Remarque : le dernier diagramme d'évolution avec un état isolé est à éviter (Hang-Up State).
Les diagrammes d'évolutions peuvent être aussi variés que ceux présentés ci-dessus. Ils peuvent avoir un ou plusieurs
cycles. La suite des états n'est pas forcément dans l'ordre naturel (du comptage). Le nombre d'états N est relié au nombre
n de bascules D : N = 2n

Si l'on veut trouver un diagramme d'évolution à partir d'un schéma utilisant des bascules D, il faut positionner les sorties
des bascules D (qui constitueront l'état présent), puis chercher ce qui en résultera sur les entrées de ces bascules (qui
constitueront l'état futur). En répétant ce travail pour chacune des possibilités en entrées on trouvera le diagramme
d'évolution.
Exercice 1
Trouver les diagrammes d'évolutions correspondant aux schémas ci-dessous :
Des diagrammes d'évolutions aux équations de récurrences
Il est facile de construire une table des transitions (état présent ; état futur) à partir d'un diagramme d'évolution. Cela
constitue tout simplement la table de vérité de l'équations de récurrence cherchée. Si on veut une forme simplifiée il
faudra utiliser un ou plusieurs tableaux de karnaugh. Par exemple pour le premier diagramme d'évolution donné en haut
de cette page, on trouve :
Tableau Etat présent/Etat futur
Etat présent Etat futur
q1 q0 Q1 Q0
0001
0110
1011
1100
On peut en déduire des tableaux de Karnaugh et donc des équations simplifiées. Ici on obtient :
et
Exercice 2
Trouver les équations de récurrence de chacun des diagrammes d'évolution présentés au début de ce TD.

Des équations de récurrence aux programmes VHDL
N
ous allons maintenant apprendre à passer des équations de récurrence aux programmes VHDL. Le compteur ci-dessus
s'écrit par exemple en VHDL:
N
otez que q0 et q1 sont déclarées en INOUT, ce qui est obligatoire pour des équations de récurrences (en fait il existe
d'autres façons de faire).
Exercice 3
Pour chacune des équations de récurrence trouvées à l'exercice 2, écrire le programme VHDL correspondant.
TD3 : Implantation matérielle avec bascules D et bascules JK
Réaliser un schéma séquentiel à partir d'un diagramme d'évolution consiste toujours à trouver une partie combinatoire.
Les raisonnements seront séquentiels, mais les méthodes employées viennent du combinatoire : tables de vérité, tableaux
de Karnaugh.
Implantations à l'aide de bascules D
Si l'on connaît les équations de récurrence, il est facile d'obtenir un schéma à l'aide de bascules D. Il suffit d'implanter les
équations de récurrence. Si on ne les connaît pas il suffit de les chercher. On présente d'abord ce que l'on cherche à
réaliser : une partie combinatoire à la place du point d'interrogation :
Exercice 1
Réaliser un compteur modulo 8 (qui compte de 0 à 7) à l'aide de 3 bascules D.
Implantation à l'aide de bascules JK
ENTITY cmpt IS PORT (
clk: IN BIT;
q0,q1: INOUT BIT);
END cmpt;
ARCHITECTURE acmpt OF cmpt IS
BEGIN
PROCESS (clk) BEGIN -- ou cmpt:PROCESS (clk) BEGIN
IF (clk'EVENT AND clk='1') THEN
q0 <= NOT q0;
q1 <= q0 XOR q1;
END IF;
END PROCESS;
END acmpt;