Polarisation de la lumière et Loi de Malus

Annexes
Polarisation de la lumière et Loi de Malus
1. Introduction
Dans le cours d’optique géométrique, le modèle utilisé pour décrire la propagation de la lumière est
celui des rayons lumineux. Bien que ce modèle nous ait permis de décrire de nombreuses situations (lois de
Descartes, propagation de la lumière à travers des lentilles, …), il révèle certaines limites, notamment lorsque
l’on s’intéresse à la description des phénomènes d’interférences ou de diffraction par exemple. Pour ces cas de
figures un peu plus complexes, il faut voir la lumière comme une onde électromagnétique. Elle est alors décrite
par la propagation de deux champs vectoriels, le champ électrique  et le champ magnétique  . Dans le vide ces
deux vecteurs ont la propriété remarquable d’être orthogonaux. De plus vous verrez l’an prochain grâce aux
équations de Maxwell que si  est la direction de propagation de l’onde électromagnétique (cas de la figure
ci-dessous) alors   forme un trièdre direct. Pour plus de clarté, dans la suite nous ne nous intéresserons
qu’au champ électrique  mais les notions sont équivalentes pour le champ magnétique. Vous verrez aussi l’an
prochain que si le champ électrique est décrit sous la forme d’une onde plane progressive harmonique (OPPH)
se propageant dans la direction  , alors, dans la base  , il peut être mis sous la forme :
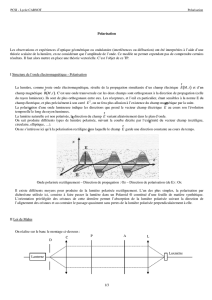
Figure 1. Exemple d’onde électromagnétique polarisée rectilignement
2. Notion de polarisation de la lumière
Pour plus de clarté, dans la suite nous ne nous intéresserons qu’au champ électrique  . Dans la figure
1, le champ électrique est polarisé rectilignement selon  : au cours de la propagation de l’onde, le vecteur 
reste dans le plan (Oxz). Ainsi la pointe du vecteur  évolue seulement dans la direction de  (selon une ligne).
Dans le cas général, la polarisation d’une onde est elliptique : la pointe du vecteur  décrit une ellipse dans le
plan (Oxy) au cours de sa propagation. En imposant certaines conditions sur la structure du champ, on peut
observer des polarisations particulières :
- polarisation circulaire si : 
 et  
- polarisation circulaire si :  (pas de déphasage entre les composantes du champ électrique)
x
y
z
x
y
x
y
x
y
elliptique
circulaire
rectiligne

Annexes
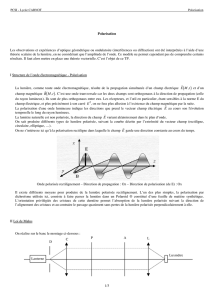
Figure 2. Onde électromagnétique polarisée circulairement : la pointe du vecteur  décrit un cercle (dans le plan
Oxy) durant sa propagation selon l’axe Oz
Souvent, la lumière n’est pas polarisée : la pointe du vecteur  ne décrit aucune forme particulière.
L’onde électromagnétique peut toutefois être décrite comme la superposition de plusieurs ondes polarisées
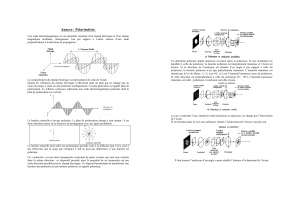
(théorème de superposition). Afin de polariser une onde qui ne l’est initialement pas, on utilise un polariseur
(dichroïque) : si une onde non polarisée arrive sur un tel objet, elle en sort polarisée rectilignement selon l’axe
du polariseur (voir figure 3).
Figure 3. Polariseur permettant de transformer une onde non polarisée une onde polarisée rectilignement.
3. Loi de Malus
On suppose une onde polarisée rectilignement selon  par exemple. On place un polariseur sur le
chemin de cette onde dont l’axe de polarisation peut varier. La loi de Malus dit alors que l’intensité lumineuse I
mesurée en aval du polariseur est donnée par :
où I0 est l’intensité lumineuse incidente et θ est l’angle que fait l’axe de polarisation du polariseur avec celui de
l’onde incidente.
Nous n’avons pas de source de lumière qui est naturellement polarisée rectilignement. Une façon commode de
créer artificiellement une telle onde est d’utiliser une source de lumière non polarisée et de la faire traverser un
premier polariseur. La lumière avale est alors polarisée selon l’axe du premier polariseur. On peut donc ensuite
l’analyser grâce à un deuxième polariseur que l’on appellera logiquement un analyseur.
x
z
x
y
x
x
y
z
Onde non polarisée = superposition d’ondes
polarisées rectilignement
Onde polarisée rectilignement dans la
direction Ox
Polariseur rectiligne
Onde incidente
polarisée
rectilignement
dans la direction
verticale
Intensité I0
Onde émergente
polarisée
rectilignement
dans la direction
« θ »
Intensité I

Annexes
Figure 4. Illustration de la loi de Malus
Remarque : expérimentalement, la quantité que l’on mesure est l’intensité lumineuse (ou l’intensité lumineuse
par unité de surface) qui mesure la puissance de l’onde lumineuse. Vous verrez en 2ème année qu’elle est
proportionnelle à l’amplitude du champ électrique au carré.
DOCUMENT : LES LUNETTES 3D
La 3D ou stéréoscopie est une image qui utilise les trois dimensions que sont la hauteur, la largeur et la
profondeur. Contrairement à une image 2D qui est plane, la 3D avec la profondeur, nous donne une impression
de relief, de perspective et de distance.
Cette impression nous est donnée naturellement grâce à notre anatomie. En effet, nos yeux, qui sont
espacés de 6,5 mm environ, ne perçoivent pas la même image mais deux images planes différentes. Un objet vu
de l’œil droit est donc vu sous un angle différent de l’œil gauche. Ces deux images sont envoyées grâce aux
récepteurs situés sur la rétine au cerveau. Ce dernier va synthétiser les deux images et les assembler en les
superposant pour nous donner une image finale en relief. Ce phénomène est appelé la parallaxe.
Pour obtenir le relief au cinéma, on tourne deux films : un pour l’œil droit, un pour l’œil gauche, à l’aide
d’une caméra stéréoscopique (comportant deux objectifs espacés comme les yeux d’environ 7 cm). Nous avons
donc deux films mais pour les visionner en 3D, il faut utiliser des lunettes spécifiques. Ces lunettes sont dites
passives si, contrairement aux lunettes actives, elles ne disposent d’aucun système électronique embarqué.
L'effet de relief sera effectif si et seulement si chaque œil voit une image différente.
La technique que nous allons présenter est la plus répandue dans nos salles de cinéma actuellement
(exemple : Avatar de James Cameron) mais surtout pour nos écrans de télévision à la maison. Elle se base sur la
polarisation de la lumière.
Afin d’obtenir de la lumière polarisée dans une seule direction, on utilise un polariseur (ou filtre
polarisant). Ce dispositif optique ne laisse passer que les composantes de la lumière qui sont polarisées dans une
direction choisie.
On projette les deux images filmées avec un léger décalage et grâce à des lunettes spécifiques possédant
les mêmes filtres polarisants que les projecteurs, chaque œil ne voit que l’image qui lui est destinée, l’autre étant
arrêtée par le filtre.
Cette technique, dite de polarisation linéaire, nécessite donc de placer un filtre polarisant simple
différent devant chaque projecteur. Les deux images filtrées atteignent ensuite l’écran simultanément où elles y
sont réfléchies, tout en gardant le décalage entre l’image ‘’gauche’’ et l’image ‘’droite’’ et renvoyées au
spectateur. A cet instant l’image est donc uniquement composée de ses composantes verticales et horizontales
(lumière bipolaire). Là interviennent les lunettes 3D où chaque verre est constitué d’un filtre polarisant différent
qui va recomposer l’image en une pour chaque œil.

Annexes