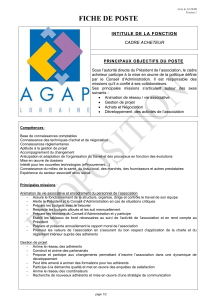
n+1=0,75u n+800 .

TES spécialité MATHEMATIQUES pour le 14-12-10
DM n°4
I) 1) Déterminer la suite de nombres que l’on obtient par chacun des procédés suivants (on calculera
6 termes), et décrire le procédé par une formule .
a) Chaque terme est obtenu en ajoutant 6 au précédent et en divisant le tout par 2 ; prendre 10
au départ .
b) Chaque terme est obtenu en ajoutant son rang au terme précédent, sachant que le terme de
départ, de rang 1, est 2 .
c) Chaque terme est obtenu en prenant 80 % du précédent et en lui ajoutant 20 % de celui
encore avant (l’antéprécédent), les deux premiers étant 100 et 200 ;
2) On donne des suites finies de nombres . Pour chacune d’elles, trouver le terme manquant (...)
possible, puis trouver le procédé de construction de la suite .
a) 38 ; 29 ; 20 ; 11 ; (...) .
b) 2 ; 3 ; 6 ; 11 ; 18 ; 27 ; (...) .
1. 0 ; 5 ; 3 ; 8 ; 6 ; 11 ; (...) ; 14 ; 12 .
II) On considère la suite u définie par
u
n
=
2
n
3
n
1
,pour tout entier naturel n .
1) Calculer les cinq premiers termes de la suite et les représenter graphiquement .
2) a) Déterminer le signe de
u
n 1
u
n
(sans donner de valeur à n)
b) Déterminer le sens de variation de la suite u
c) En déduire que la suite est majorée par 3 .
3) Déterminer le signe de
u
n
2
; que peut-on en déduire pour la suite u ?
III) le président d’une association sportive constate que, chaque année, l’association garde 75 % de
ses anciens adhérents et qu’il y a 800 nouveaux adhérents . En l’année 2000, l’association avait
1600 adhérents. On veut prévoir l’évolution du nombre d’adhérents en supposant que la tendance
observée va se poursuivre . Pour cela, on modélise la situation en utilisant une suite
u
n
,
u
n
étant le nombre d’adhérents de l’année (2000+ n) .
On a donc
u
0
=
1600
.
1) Calculer le nombre d’adhérents en 2001, puis en 2002 .
2)a) Montrer que
u
n
1
=
0,75
u
n
800
.
b) Calculer les dix premiers termes de la suite (on donnera les résultats au centième près)
c) A partir de quelle année le nombre d’adhérents aura-t-il augmenté de 75 % ?
3) On pose
v
n
=
3200
u
n
:
a) Calculer
v
0
.
b) Montrer que
v
n
1
=
0,75
3200
u
n
; en déduire que la suite
v
n
est une suite
géométrique dont on précisera la raison et le premier terme .
c) Déterminer le sens de variation de
v
n
et en déduire le sens de variation de
u
n
.