Exercices amplificateur differentiel a transistors

1
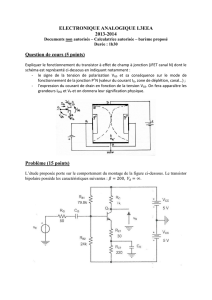
1AMPLIFICATEUR DIFFERENTIEL A TRANSISTORS JFET
On considère le montage amplificateur différentiel de la figure 1a qui utilise deux
transistors JFET canal N identiques, soumis à la même température T de 25°C. Ils fonctionnent
dans la zone de « plateau » de leur caractéristique de sortie où :
II V
VImAVV
DDSS
GS
P
DSS P
=−
==−112 2
2
( )
- VEE = -15 V
V
E
R
2.I0
RD
ID1 ID2
T1T2
G1
G2
S
D1
D2
+ VCC = +15 V
VE2
RD
10kΩ
10kΩ
VE1
VS1
VS2
2 1.5 1 0.5 0
0
0.5
1
1.5
2
VGS (V)
ID (mA)
I0
I0-∆I
V
E
I0+∆I
IDSS
Figure 1a Figure 1b
1° PARTIE : POLARISATION
On relie les grilles G1 et G2 à la masse de manière à obtenir une tension d’entrée VE nulle.
• Montrer que les tensions VG1S et VG2S sont égales.
• En déduire la valeur à donner à la résistance R pour polariser T1 et T2 avec un courant de
drain tel que : ID1repos = ID2repos = I0 = 0.5 mA.
• Donner le potentiel de tous les noeuds du schéma par rapport à la masse.
2° PARTIE : AMPLIFICATION D'UNE DIFFERENCE DE TENSIONS CONTINUES
On désire connaître les performances du montage aux grands signaux continus appliqués entre les
grilles G1 et G2. A cet effet, on attaque la paire différentielle T1 T
2 avec une tension continue VE
positive telle que : VE = VE1 - VE2 = VG1S - VG2S..
Si on appelle
∆ I l’augmentation du courant de drain de T1 vis-à-vis du courant de repos I0, on peut
écrire tant que le fonctionnement est linéaire (figure 1b) : ID1 = I0 + ∆I ID2 = I0 - ∆I.
1 Ph.ROUX © 2006

2
2.1) On se propose de déterminer l’expression de la variation de courant ∆I en fonction de VE.
• Rechercher d'abord l'expression de la tension d'entrée VE en fonction de IDSS, I0, ∆I et VP.
• En déduire l'expression de l'accroissement de courant de drain ∆I en fonction de VE sous la
forme suivante (il faut élever successivement deux fois au carré) :
∆IGV aV
md E E
=−1
2
• Etablir l’expression de la transconductance différentielle Gmd et du coefficient a. A.N.
Le graphe de l'évolution des courants ID1 et ID2 en fonction de la tension VE variant de - 1,5 à +1,5
volt est donné en figure 2.
1.5 1.25 1 0.75 0.5 0.25 0 0.25 0.5 0.75 1 1.25 1.5
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
ID1 (VE)
ID2 (VE)
VE en volt
0.283 0.283
Figure 2
2.2) On désire rester dans la zone linéaire où ∆ I reste proportionnel à VE avec une erreur relative
au plus égale à 1%.
• En utilisant l'approximation
11
2
−≈−xx
, calculer la valeur VEmax admissible.
• En déduire la relation reliant alors la différence des tensions de sortie VS1 - VS2 à la tension
d’entrée différentielle VE et conclure.
3° PARTIE : ETUDE AUX PETITES VARIATIONS
On excite maintenant le montage par deux tensions sinusoïdales ve1 et ve2 de même fréquence
et telles que l'amplitude de leur différence ve respecte la limite de linéarité précédemment définie.
3.1) Dessiner le schéma équivalent au montage complet aux petites variations et aux fréquences
moyennes, la résistance interne rds de T1 et T2 étant négligeable.
3.2) Calculer le gain différence
Avv
vv
d
ss
ee
=−
−
12
12
du montage ainsi que le gain en mode commun
Avv
vv
c
ss
ee
=+
+
12
12
et le (R)apport de (R)éjection du (M)ode (C)ommun
A
A
d
c
exprimé en déciBels.

3
3.3) Application : On décide d’utiliser exclusivement la tension de sortie vs2 (utilisation en mode
asymétrique).
Sachant que les tensions d’entrée ve1 et ve2 ont une amplitude respective de 1.1 V et 1V :
• Calculer l’expression de la tension de sortie vs2. Faire l’application numérique.
• Calculer l’erreur relative entre la valeur de vs2 obtenue avec un RRMC infini et celui de la
question 3.2. Conclure.
4 ° PARTIE : AMELIORATION DU R.R.M.C.
On améliore le R.R.M.C. du montage en remplaçant la résistance de polarisation R par un
générateur de courant continu de résistance interne Ri (figure 3a). Ce générateur est réalisé par le
montage T3, T4 et R2 de la figure 3b. Il s’agit d’un miroir de courant à transistors bipolaires
identiques munis d'une résistance R2 = 5 K Ω dans leur émetteur. Les transistors T3 et T4 sont tels
que :
ββ
ββ
= 100, tension de Early VA = - 160 V.
On supposera que le miroir de courant assure la relation IC4 = IC3.
10 kΩ 10 kΩ
+ VCC = +15 V
- VEE = -15 V
ve
2
ve
1
v
e
T1T2
2I0R
i
S
R
D
R
D
vs
2
10 kΩ 10 kΩ
+ VCC = +15 V
- VEE = -15 V
ve
2
ve1 v
e
T1T2
2I0
S
R
D
R
D
vs
2
5 kΩ 5 kΩ
R2R2
R1
T4T3
Figure 3a Figure 3b
4.1) Déterminer la valeur à donner à la résistance R1 pour conserver la même valeur du gain
différence Ad (négliger le courant de base des transistors T3 et T4).
4.2) En utilisant la méthode de l’ohmmètre, calculer la résistance interne Ri du montage miroir de
courant vue par les JFET T1 et T2 entre leur source et la masse. A cet effet, on simulera au préalable,
le transistor T3 monté en diode (B et C court-circuités) par une résistance r3 telle que :
rgm
3
3
1
≈
4.3) En déduire la nouvelle valeur du gain de mode commun et du R.R.M.C. et reprendre la
question 3.3 de la troisième partie.

4
CORRECTION
1° PARTIE : POLARISATION
Exprimons la tension d’entrée VE : VE = VG1S – VG2S. Une tension d’entrée nulle entraîne donc :
VG1S = VG2S et par voie de conséquence : ID1repos = ID2repos .
Calculons la tension VGS :
VV I
I
GS P
DSS
=±
10
.
Nous obtenons deux solutions pour I0 = 0,5 mA : VGS = -1 et –3 V. On retient VGS = -1 V en effet
l’autre solution correspond au blocage du JFET.
La tension VSM est alors égale à 16 V, ce qui conduit à R = 16 KΩ.
10 kΩ 10 kΩ
+ VCC = +15 V
- VEE = -15 V
v
e
T1T2
R
S
R
D
R
D
1 V
0,5mA
0,5mA
10 V 10
V
1 mA
16 KΩ
2° PARTIE : AMPLIFICATION D'UNE DIFFERENCE DE TENSIONS CONTINUES
2.1) Expression de la tension d’entrée : VE = VG1S – VG2S avec :
VV II
I
GS P
DSS
1
0
1=−
+
∆
et
VV II
I
GS P
DSS
2
0
1=−
−
∆
->
VV II
I
II
I
EP
DSS DSS
=−−+
00
∆∆
Pour exprimer ∆I, il faut élever deux fois au carré, on obtient alors :
∆III
VVI IV V
DDSS
P
E
DSS
P
E
=−
() .14
0
2
• Transconductance différentielle :
GII
VmS
md
D DSS
P
==(),05
• Coefficient :
aI
IV V
DSS
P
==
−
4025
0
2
2
,

5
2.2) On utilise l’approximation :
∆IGV aV GV aV
md E E md E E
=−≈−11
1
2
22
()
Pour une erreur relative de 1%, on doit assurer :
1
2
1
100
2
aVE=
qui a pour solution :
VEmin = -0,283 V et VEmax = + 0,283 V. On a alors :
∆IGV
md E
=
.
3° PARTIE : ETUDE AUX PETITES VARIATIONS
3.1) Schéma aux variations :
R
R
D
R
D
S
G1G2
vgs1 vgs
2
ve
gm.vgs1 gm.vgs2
D2
vs1
D1
vs
2
ve1 ve2
3.2) Calcul du gain différence
Avv
vv
d
ss
ee
=−
−
12
12
vv v
egs gs
=−
12
vgvR
s m gs D11
=− vgvR
s m gs D22
=−
->
vv gRv v
s s m D gs gs12 1 2
−=− −()
Avv
vgR
d
ss
e
mD
=−=−
12.
Transconductance :
gVII mS
m
P
D DSS
repos
=− =
21.
A
d = -10 .
Calcul du gain de mode commun
Avs v
vv
c
s
ee
=+
+
12
12
:
vv gRv v
s s m D gs gs12 1 2
+=− +()
v Rgv gv
emgsmgs112
=+()
v Rgv gv
e m gs m gs212
=+()
Soit :
vv gRv v
ee mgsgs12 1 2
2+= +()
Avv
vv
gR
gR
c
ss
ee
mD
m
=+
+=− +=−
12
1212 0 303,
RRMC A
Ag R soit dB
d
c
m
. . . . ==+ =1 2 33 30
3.3) Seule la sortie vs2 est utilisée. Elle s’exprime en utilisant les expressions de Ad et Ac :
vAvvAvv
sdeecee21212
1
2
1
2
=− − + +()()