Exercices montage amplificateur en emetteur

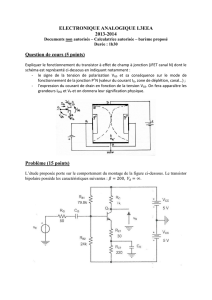
MONTAGE AMPLIFICATEUR EN EMETTEUR COMMUN “BOOTSTRAP”
+ VCC = + 20V
+
-
eg
C1
C2
C3
R1
R2
R3
RE
RC
K
Ru
vevs
10 kΩ
330 kΩ
33 kΩ
4,7 kΩ
470 Ω
10 kΩ
M
B
C
E
Rg
1 kΩ
A
v= vs
ve
MONTAGE AMPLIFICATEUR EN EMETTEUR COMMUN “BOOTSTRAP”
Le schéma du montage à étudier est donné en figure 1. Il utilise un transistor NPN à 25 °C dont les
paramètres sont les suivants :
ββ
ββ = 500, VBE = 0.6 V, ICrepos = 2 mA et résistance rce infinie
+ VCC = + 20V
+
-
eg
C1
C2
C3
R1
R2
R3
RE
RC
K
Ru
vevs
10 kΩ
330 kΩ
33 kΩ
4,7 kΩ
470 Ω
10 kΩ
M
B
C
E
Rg
1 kΩ
1° PARTIE : On suppose que l’interrupteur K est ouvert.
(1) Sachant que dans le domaine des fréquences de travail, tous les condensateurs sont des courts-
circuits, dessiner le schéma équivalent au montage complet, aux petites variations et aux fréquences
moyennes. On choisit de représenter le transistor par son modèle en “ββ
ββ ib”
(2) Déterminer l’expression de la résistance d’entrée Re vue par le générateur d’attaque (eg, Rg).
Ne pas oublier de donner le schéma d’analyse. Faire l’application numérique.
2° PARTIE : On suppose que l’interrupteur K est fermé.
Le condensateur “bootstrap” C2 va ramener, aux variations, le pont de polarisation R1 R2 dans le
circuit d’émetteur du transistor. Cette technique va entraîner une augmentation de la résistance
d’entrée du montage.
(3) Sachant que dans le domaine des fréquences de travail, tous les condensateurs sont des courts-
circuits, dessiner le schéma équivalent au montage complet, aux petites variations et aux fréquences
moyennes. Représentez le transistor par son modèle en “gm vbe”.
On appelle r la résistance équivalente située entre base et émetteur du transistor et Réq celle qui se
trouve entre collecteur et masse et R’E entre émetteur et masse.
(4) Calculer l’expression du gain en tension du montage :
A
v= vs
ve
. Faire l’application numérique.
(5) Déterminer l’ expression de la résistance d’ entrée Re vue par le générateur d’attaque (eg, Rg).
Faire l’application numérique.
(6) Déterminer l’expression de la résistance de sortie Rs du montage vue par la résistance Ru.
Ne pas oublier de donner le schéma d’analyse. Faire l’application numérique.

CORRIGE
Q1 : K est ouvert. Schéma équivalent au montage complet :
eg
+
-
R
g
R
2
R
1//
R
3
R
E
β.i
b
R
c//
R
u
v
e
v
s
ib BEC
r
be
ig
Q2 : Résistance d’entrée Re vue par le générateur d’attaque (eg, Rg).
Rv
iRRR r R
ee
gbe E
== + ++( // ) //( ( ) )
213 1
β
avec :
rU
Ik
be T
Crepos
== β 625,Ω
Re = 33,7 kΩ
Q3 : K est fermé. Schéma équivalent au montage complet :
eg
+
-
R
g
R’
E
gm.v
b
e
R
eq = Rc //Ru
v
e
v
s
ig
B
EC
v
be
r
be
R
2
r
R’
E = R1 //R3//RE
Req
Q4 : Calculer l’expression du gain en tension du montage :
vRgv
seqmbe
=− ..
vv R
vrgv
ebeE
be mb
e
=+ +
©
(.)
AgR
Rrg
vmeq
Em
=−
++
=−
.
()
,
©
1167

Q5 : Résistance d’entrée Re vue par le générateur d’attaque (eg, Rg).
Rv
irR gr k
ee
gEm
==+ + =
©
(.)1 147 Ω
Intérêt du montage : permet d’augmenter de façon significative la résistance d’entrée (33kΩ à 147
kΩ) en plaçant une partie du circuit de polarisation en parallèle avec RE. En effet, toute résistance
entre E et masse est vue de la base, sensiblement multipliée par le gain en courant β du transistor.
En outre le gain en tension est peu affecté.
Q6 : Résistance de sortie Rs du montage vue par la résistance Ru. Méthode de « l’ohmmètre » :
ne pas oublier de court-circuiter eg et d’enlever la résistance Ru. Le schéma est alors le suivant :
R
g
R’
E
gm.v
b
e
B
EC
v
be
r
be
R
2
r
R’
E = R1 //R3//RE
Rc u
+
-
i
En écrivant l’équation de la maille d’entrée on obtient la relation :
vg
rR
rR R
be m E
gE
(.)
©
©
10+++ =
donc la tension de commande vbe est nulle.
Le générateur dépendant (gm.vbe) est aussi nul. Dans ces conditions : Rs = RC.