LEÇON N˚ 39 : Réflexions du plan échangeant

LEÇON N˚ 39 :
Réflexions du plan échangeant deux
droites sécantes données, bissectrices.
Applications au triangle et au cercle (cercle
inscrit, tangente à un cercle, ...).
Pré-requis :
–Géométrie affine et vectorielle;
–Médiatrice, barycentre;
–Projection orthogonale, réflexion : définitions et propriétés.
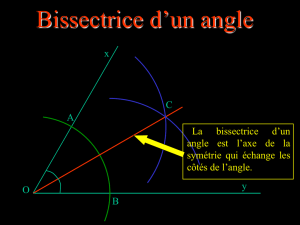
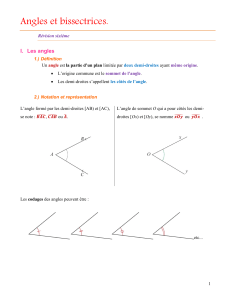
On se place dans un plan affine euclidien P(les angles orientés sont inutiles). Au collège, la bissectrice
d’un angle géométrique est définie comme étant un axe de symétrie.
39.1 Réflexions et bissectrices
39.1.1 Bissectrices de deux droites
Théorème 1 : Soient Det D′deux droites de Psécantes en un point O. Il existe exactement deux
réflexions échangeant Det D′. Leurs axes sont perpendiculaires et passent par O.
démonstration :
Analyse : Soit ∆une droite telle que s∆(D) = D′. Puisque D∩D′={O},s∆({O}) = s∆(D∩D′) =
s∆(D)∩s∆(D′) = D′∩D={O}. Soient alors A∈Ddifférent de Oet A′son image par s∆. Alors
OA =OA′, de sorte que A′∈D′∩C(O, OA). D’où deux points possibles, notés A1et A2. On pose
alors ∆1(resp. ∆2) la médiatrice de [AA1](resp. [AA2]).
Synthèse : s∆1(O) = Oet s∆1(A) = A1impliquent s∆1(D) = s∆1(OA) = (OA′) = D′, et l’on
montre de même que s∆2(D) = D′. De plus, [AA2]est un diamètre du cercle Cdéfini plus haut,
contenant A1, donc le triangle A1AA2est rectangle en A. Or (AA1)⊥∆1et (AA2)⊥∆2, donc
∆1⊥∆2.
Exercice : Montrer que si −→ uet −→ vsont respectivement des vecteurs unitaires de Det D′, alors les axes de
symétrie sont dirigés par −→ u±−→ v.
Convenons tout d’abord −→ u=−→ OA/k−→ OAket −→ v=−−→ OA1/k−−→ OA1k(ce qui implique d’ailleurs que −−→ v=−−→ OA2/k−−→ OA2kpar construc-
tion de A1et A2).

2Réflexions du plan échangeant deux droites sécantes
−→
u+−→ v:On a les égalités suivantes :
−−→
AA1·(−→ u+−→ v) = −−→ AA1·−→ OA/k−→ OAk+−−→ OA1/k−−→ OA1k=1
k−→ OAk(−−→
0A1−−→
OA)·(−→
OA +−−→
OA1)
=1
k−→ OAkk−−→
OA1k2− k−→ OAk2= 0.
−→
u−−→ v:On montre de même que :
−−→
AA2·(−→ u−−→ v) = −−→
AA2·−→
OA/k−→
OAk+−−→
OA2/k−−→
OA2k=1
k−→ OAkk−−→
OA2k2− k−→
OAk2= 0.
Dans ces égalités, nous avons évidemment utilsé le fait que k−→ OAk=k−−→ OA1k=k−−→ OA2k.♦
Proposition 1 : ∆1∪∆2={M∈P|d(M, D) = d(M, D′)}.
démonstration :
"⊂" : Soit M∈∆1∪∆2. Si M=O, alors il est évident que d(M, D) = d(M, D′) = 0. Supposons
alors M6=O.
On peut considérer M∈∆1. Soient Ple projeté orthogonal de Msur
D, de sorte que d(M, D) = M P , et P′=s∆1(P). Alors P′∈D′et
MP =MP ′(en effet, s∆1(M) = M). Par suite, s∆1(MP ) = (MP ′), et
puisque s∆1conserve l’orthogonalité, on a l’implication D⊥(MP )⇒
D′⊥(MP ′), donc P′est le projeté orthogonale de Msur D′et réalise
donc le minimum de la distance de Mà la droite D′, c’est-à-dire MP ′=
d(M, D′).
OM
P
P′
D
D′
∆
"⊃" : Soit M∈Ptel que d(M, D) = d(M, D′). Soient P(resp. P′) le projeté orthogonal de Msur
D(resp. D’) et dla médiatrice de [P P ′]. Alors M∈dcar d(M, D) = d(M, D′)⇔M P =
MP ′. On en déduit que sd(D) = D′, donc dest l’une des deux bissectrices ∆1ou ∆2.
39.1.2 Réflexion de demi-droites
Définition 2 : Soient Det D′deux droites sécantes en un point O,A∈Det B∈D′deux
points disctints de O. On appelle bissectrice intérieure de l’angle \ AOB la droite notée ∆1telle que
s∆1[OA)= [OB). La droite ∆2, perpendiculaire à ∆1passant par Oest alors appelée bissectrice
extérieure de l’angle \ AOB.
Remarque 1 :Si −→ uet −→ vsont respectivement des vecteurs directeurs des droites Det D′, alors ∆1(resp. ∆2) est
dirigée par −→ u+−→ v(resp. −→ u−−→ v).
39.2 Application au triangle et au crecle
39.2.1 Cercle inscrit et exinscrit
Définition 3 : Soit ABC un triangle non plat de P. Les bissectrices intérieures (resp. extérieures) du
triangle ABC sont les bissectrices intérieures (resp. extérieures) des angles \ BAC,\ ACB et \ CBA.

Réflexions du plan échangeant deux droites sécantes 3
Théorème 2 : Dans un triangle ABC non plat, les trois
bissectrices intérieures sont concourantes en un point I,
barycentre du système {(A, a),(B, b),(C, c)}(où a=
BC, b =AC et c=AB). C’est le centre du cercle ins-
crit au triangle.
A
B
C
I
démonstration :Soit Ile barycentre du système {(A, a),(B, b),(C, c)}(on remarque que ABC non
plat ⇒a+b+c6= 0). On a donc :
∀M∈P,−−→ MI =1
a+b+c(a−−→
MA +b−−→ MB +c−−→ MC)
M=A
⇒−→ AI 1
a+b+c(b−−→
AB +c−→ AC) = bc
a+b+c −−→
AB
k−−→ ABk+
−→
AC
k−→ ACk
|{z }
=: −→ u
!.
Donc −→ AI et −→ usont colinéaires. Mais −→ uest un vecteur directeur de la bissectrice intérieure issue de
l’angle b A, donc (AI)n’est autre que cette bissectrice. On procède de la même manière avec M=Bet
M=Cpour en déduire que Iest bien le point d’intersection des trois bissectrices intérieures.
Par ailleurs, en notant H(resp. K, L) le projeté orthogonal de Isur (BC)(resp. (AC)et (AB)), on
montre que les triangles AIK et AIL sont isométriques (en effet, il ont un côté en commun [sur la
bissectrice issue de b A], un angle droit chacun et un autre angle identique [grâce à la bissectrice]), donc
que IK =IL. De la même manière, on trouve IL =IH. Le cercle de centre Ipassant par ces trois
points est défini de manière unique, et il est tangent aux trois côtés du triangle (par construction de
H, K et L), donc c’est bien le cercle inscrit. 
Théorème 3 : Soit ABC un triangle non plat. La bissectrice intérieure issue de b A(resp. b B, b C) et les-
bissectrices extérieures issues des deux autres angles sont concourantes en un point IA(resp. IB, IC)
qui est le centre du cercle exinscrit relatif au premier sommet. De plus, IAest le barycentre du sys-
tème {(A, −a),(B, b),(C, c)}(resp. IBest le barycentre du système {(A, a),(B, −b),(C, c)},
ICest le barycentre du système {(A, a),(B, b),(C, −c)}).
démonstration :Soit Ile barycentre du système {(A, −a),(B, b),(C, c)}(on remarque que ABC non
plat ⇒b+c−a6= 0). On a donc :
∀M∈P,−−→ MI =1
b+c−a(−a−−→
MA +b−−→ MB +c−−→ MC)
M=A
⇒−→
AI 1
b+c−a(b−−→
AB +c−→ AC) = bc
b+c−a −−→
AB
k−−→ ABk+
−→
AC
k−→ ACk
|{z }
=: −→ u
!.
Donc −→ AI et −→ usont colinéaires. Mais −→ uest un vecteur directeur de la bissectrice intérieure issue de
l’angle b A, donc (AI)n’est autre que cette bissectrice. Avec M=Bet M=C, on trouvera par ce
calcul un signe −dans la parenthèse, qui prouve que (BI)et (CI)sont les bissectrices extérieures. La
conclusion quant au cercle se traite de la même manière que dans le théorème précédent. 

4Réflexions du plan échangeant deux droites sécantes
Illustrons ceci par une figure :
A
B
C
I
IA
IB
IC
Remarque 2 :Iest l’orthocentre du triangle IAIBIC. En effet, (IBIC)est la bissectrice extérieure issue de b Aet
(AI)∋IAsa bissectrice intérieure. Le théorème 1 nous assure qu’elle sont perpendiculaires, de sorte que Isoit bien
sur hauteur issue de IAdu triangle IAIBIC. De même pour les autres côtés IAICet IAIB.
39.2.2 Tangente à un cercle
Proposition 2 : Soit M∈P, extérieur à un cercle C(Ω, r)donné. Il y a exactement deux tangentes
àCpassant par M. De plus, si l’on note Tet T′les intersections avec C, alors la doite (ΩM)est la
bissectrice intérieure de l’angle \ T M T ′.
démonstration :La réflexion d’axe (ΩM)conserve le cercle, puisque cette droite porte un diamètre
du cercle. Notons T1=s(ΩM)(T)∈C.(ΩT)⊥(T M), donc par conservation de l’orthogonalité, on a
s(ΩM)(ΩT)⊥s(ΩM)(T M)⇔(ΩT1)⊥(T1M). Or T1∈C, donc T1=T′, et (ΩMest la bissectrice
intérieure de l’angle \ T MT ′.
Remarque 3 :Pour mieux se représenter la chose, considérer que Cest le plus grand cercle de la figure page
précédente, Ω = IAet M=A. Alors (ΩM) = (AIA)qui est bien la bissectrice intérieure de l’angle b A.

Réflexions du plan échangeant deux droites sécantes 5
39.2.3 Rapport de longueur
Proposition 3 : Soient ABC un triangle non plat, IA(resp. JA) le pied de la bissectrice intérieure
(resp. extérieure) issue de b A. Alors on a l’égalité
AB
AC =BIA CIA
=BJA
CJA
.
démonstration :Soit HAle pied de la hauteur issue de A. Soient Ket L(resp. K′et L′) les projetés
orthogonaux de IA(resp. JA) sur (AB)et (AC)(voir figure ci-dessous). On a alors que KIA=LIA
et K′JA=L′JA(les triangles ALIAet AKIAsont isométriques, de même que mes triangles AK′JA
et AL′JA). Alors d’une part
A(ABIA)
A(ACIA)=
1
2AB ·KIA
1
2AC ·LIA
=AB
AC et A(ABIA) A(ACIA)=
1
2BIA·AHA
1
2CIA·AHA
=BIA
CIA
.
D’autre part,
A(ABJA)
A(ACJA)=
1
2AB ·K′JA
1
2AC ·L′JA
=AB
AC et A(ABJA) A(ACJA)=
1
2BJA·AHA
1
2CJA·AHA
=BJA
CJA
.
Voici la figure correspondante :
A
C
BIA
JA
KL
K′
L′
HA