Champ magnétique

I1 Champ magnétique
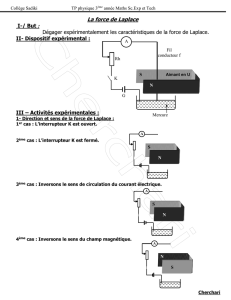
Exercices de cours
Exercice 1 Fil rectiligne dans un champ uniformeExercice 1 Utiliser l’expression de la force de Laplace
On considère un fil électrique de longueur lparcouru par un courant iplongé dans un champ magnétique uniforme et constant −→ B. On
oriente le fil selon le sens conventionnel du courant. On note A et B les extrémités du fil dans le sens conventionnel du courant et −→ AB =−→ l.
On pourra supposer que le fil est le long d’un axe A,−→ ex.
Déterminer la force de Laplace ressentie par le fil.
Exercice 2 Rails de LaplaceExercice 2 Calculer la force de Laplace
Évaluer la puissance des forces de Laplace
On considère un circuit rectangulaire constituée de deux rails
et d’une tige de longueur let de masse mmobile sans frottements
uniquement le long de l’axe −→ ex. On notera sa vitesse de translation
−→
v(t) = v(t)−→ ex.
On plonge l’ensemble dans un champ magnétique −→ Buniforme
vertical ascendant selon l’axe −→ ez.i
D
C
l
−→
B
−→
g
y
zx
(1) Établir l’équation du mouvement de la barre et la résoudre en supposant que l’intensité du circuit est constante et que la vitesse
initiale est nulle.
(2) Déterminer la puissance des actions de LAPLACE s’exerçant sur la barre
(3) Vérifiez que l’on retrouve le résultat de la question 1 avec le théorème de la puissance cinétique.
Exercice 3 Spire rectangulaireExercice 3 Établir l’expression du couple des actions de Laplace sur ce cas particulier
x
z
−→
B
O
S
P
Q
R
i
b
a
y
zx
PQ
i
SR
−→
n
θ
α
−→
B
−→
er
On considère un circuit rectangulaire PQRS de cotés aet bparcouru par un courant électrique d’intensité i. Ce circuit peut pivoter autour
de l’axe z. Il est plongé dans un champ magnétique uniforme et constant −→ B=B−→ exorthogonal à l’axe x.
(1) Montrer que la résultante des forces de Laplace sur le cadre est nulle.
(2) Calculer le moment de la force de Laplace en O pour chacun des quatre fils. En déduire le moment de force −−→ MOque ressent la spire
dans ce champ magnétique.
(3) Exprimer le moment magnétique −→ mde la spire. Trouver la relation vectorielle qui existe entre −→ m,−→ Bet −−→ MO.
1