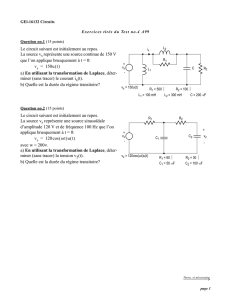
Transformation de Laplace

Transformation de Laplace
Tout comme en régime permanent sinusoïdal, l'analyse temporelle des circuits
linéaires en régime transitoire nécessite la résolution d'équations différentielles. Dans le cas
du régime sinusoïdal l'écriture et la résolution de ces équations peuvent être évitées en
travaillant dans le domaine des fréquences, en utilisant le concept des impédances. Dans ce
chapitre nous allons introduire un outil mathématique puissant, la transformation de Laplace,
pour l'étude des circuits linéaires en régime transitoire. Cette transformation permet d'associer
à toute fonction du temps f(t) une fonction F(p) d'une variable complexe p = σ + j ω. Elle
permet de remplacer les opérations analytiques de dérivation et d'intégration par des
opérations algébriques. Cette propriété facilite la résolution des équations différentielles.
L'application de la transformation de Laplace permet de plus d'avoir à écrire ces équations.
III.1 Définition et propriétés
III.1.a Définition
Dans la pratique nous avons à étudier le comportement d'un circuit en réponse à une
excitation débutant à un instant donné. Nous pouvons choisir cet instant comme origine
temporelle. Compte tenu du principe de causalité nous pouvons nous limiter à l'étude de
fonctions f(t) définies à partir de t = 0 et identiquement nulles avant :
0t0)t(f <∀=
Une telle fonction est dite causale.
Nous définissons la transformation de Laplace d'une telle fonction du temps f(t) par
l'intégrale suivante :
ω+σ=== ³∞−jpavecdte)t(f)p(F)]t(f[L 0
pt
La transformation inverse est donnée par :
³
ω
+
ω−
−π
== jc
jc
pt1 dpe)p(F
j21
)t(f)]p(F[L
En pratique nous n'utiliserons jamais cette formule. Il existe en effet des formulaires
fournissant les transformées d'un grand nombre de fonctions et donc leurs inverses. Nous
avons rassemblé en appendice une table des transformées de Laplace les plus usitées.

Une fonction simple définie à partir de t = 0 est la fonction échelon, ou Heaviside,
notée H(t) et représentée sur la figure 1 :
¯
®
>∀ <∀
=0t1
0t0
)t(H
Le produit de toute fonction par H(t) est ainsi définie uniquement pour t > 0. Il est facile de
calculer la transformée de Laplace de la fonction échelon en utilisant la définition :
p
1
e
p
1
dtedte)t(H)]t(H[L 0
pt
0
pt
0
pt =
»
¼
º
«
¬
ª−=== ∞
−
∞− ∞−³³
H(t)
t
1
0
Figure 1
III.1.b Linéarité
Etudions quelques propriétés utiles de la transformation de Laplace. Tout d'abord
remarquons que la transformation de Laplace est une application linéaire. Calculons la
transformée de la fonction g(t) = λ1 f1(t) + λ2 f2(t) :
³³³ ∞−
∞− ∞−λ+λ=λ+λ= 0
pt
22
0
pt
11
0
pt
2211 dte)t(fdte)t(fdte)]t(f)t(f[)]t(g[L
Donc : )]t(f[L)]t(f[L)]t(f)t(f[L 22112211 λ+λ=λ+λ
III.1.c Différentiation et intégration
Une propriété essentielle pour la résolution des équations différentielles concerne la
transformée de la dérivée d'une fonction :
³∞−
=
»
¼
º
«
¬
ª
0
pt dte
dt )t(fd dt )t(fd
L

Intégrons par partie :
[]
³∞−
∞
−+=
»
¼
º
«
¬
ª
0
pt
0
pt dtep)t(fe)t(f
dt )t(fd
L
Donc, sous réserve que lorsque t tend vers l'infini la fonction f(t) diverge moins vite qu'une
exponentielle, ce qui est le cas pour toutes les "bonnes" fonctions physiques, nous avons :
)0(f)p(Fp
dt )t(fd
L0e)t(fLim pt
t−=
»
¼
º
«
¬
ª
=
−
∞→
Nous pouvons généraliser ce résultat. Par exemple pour la dérivée seconde :
dt )0(fd dt )t(fd
Lp
dt )t(fd dt
d
L
dt
)t(fd
L2
2−
»
¼
º
«
¬
ª
=
¿
¾
½
¯
®
»
¼
º
«
¬
ª
=
»
»
¼
º
«
«
¬
ª
dt )0(fd
)0(fp)p(Fp
dt )0(fd
)]0(f)p(Fp[p
dt
)t(fd
L2
2
2−−=−−=
»
»
¼
º
«
«
¬
ª
De manière générale :
k
k
)k(
1n
0k
)k(k1nn
n
n
dt
)0(fd
)0(favec)0(fp)p(Fp
dt
)t(fd
L=−=
»
»
¼
º
«
«
¬
ª¦
−
=
−−
Inversement, considérons la transformation de Laplace de la primitive d'une fonction f(t) :
³³³∞−
»
»
¼
º
«
«
¬
ª
=
»
»
¼
º
«
«
¬
ª
0
pt
t
0
t
0dtedu)u(fdu)u(fL
Intégrons par partie :
³³³ ∞−
∞
−+
»
»
¼
º
«
«
¬
ª−=
»
»
¼
º
«
«
¬
ª
0
pt
0
t
0
pt
t
0dte
p
1
)t(fdu)u(fe
p
1
du)u(fL
Avec la même réserve sur le comportement de la primitive de la fonction f(t) lorsque t tend
vers l'infini, nous obtenons :
)p(F
p
1
du)u(fL t
0=
»
»
¼
º
«
«
¬
ª³

Considérons la dérivée par rapport à p de la transformée de Laplace d'une fonction f(t) :
³∞−
=0
pt dte)t(f
dp
d
dp )p(Fd
Comme la variable p n'apparaît que dans l'exponentielle nous avons :
³³ ∞−
∞−−== 0
pt
0
pt dte)t(ftdt
dp
ed
)t(f
dp )p(Fd
Soit encore :
dp )p(Fd
)]t(ft[L −=
III.1.d Translations
Considérons la transformation suivante :
³³ ∞+−
∞−−− == 0
t)ap(
0
ptatat dte)t(fdte)t(fe)]t(fe[L
Donc :
)ap(F)]t(fe[L at +=
−
Considérons la transformée d'une fonction décalée dans le temps :
³³ ∞−
∞−−=−−=−− a
pt
0
pt dte)at(fdte)at(H)at(f)]at(H)at(f[L
où H(t) est la fonction échelon. En effectuant le changement de variable x = t − a, il vient :
³³ ∞−−
∞+− ==−− 0
pxpa
0
)ax(p dxe)x(fedxe)x(f)]at(H)at(f[L
Donc :
)p(Fe)]at(H)at(f[L pa−
=−−
Nous allons utiliser cette propriété pour calculer la transformée d'une fonction périodique à
partir de t = 0.

III.1.e Transformée d'une fonction périodique
Considérons une fonction périodique de période T pour t > 0 et identiquement nulle
pour t < 0 :
f(t)
t
0 T 2T 3T
Figure 2
La fonction f(t) peut être vue comme une somme de fonctions définies chacune sur une
période :
¦
∞
=
=+++=
1
k
k321 )t(f...)t(f)t(f)t(f)t(f
La fonction f1(t) se confond avec f(t) sur la première période [0, T] et est nulle à l'extérieur :
f (t)
t
0 T 2T 3T
1
Figure 3
La fonction f2(t) est définie sur la seconde période [T, 2T].
f (t)
t
0 T 2T 3T
2
Figure 4
Elle se déduit de la fonction f1(t) par un décalage d'une période :
)Tt(H)Tt(f)Tt(f)t(f 112 −−=−=