energie cinétique

0
500
1000
1500
2000
2500
3000
0123456
Exercice 1 : Travail d’une force.( 7 points )
Un brancardier ramène un patient dans sa chambre sur un chariot roulant.
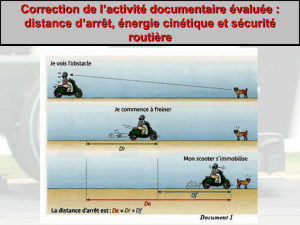
1. Dans une première étape, il parcourt un couloir de 15 mètres de long dont le sol est horizontal. La masse
de l’ensemble chariot + patient est égal à 60 kg. Les forces appliquées au système sont le poids, la force
de poussée du brancardier la force de frottement des roues sur le sol et la force exercée par le sol.
1.1. Sur le schéma suivant, identifier chacune de ces forces.
1.2. Sans faire de calcul, justifier le fait que la force de
poussée exerce un travail positif.
1.3. Justifier le fait que le travail des forces P et R
N
est nul.
1.4. Calculer les travaux des forces F et f.
Données : f = 20 N et F = 100 N.
2. Dans un second temps, le brancardier prend l’ascenseur. Il monte le patient du premier au troisième
étage. Calculer le travail du poids pendant le mouvement, si on considère que monter un étage revient à
s’élever de 2,50 m.
Exercice 2. Freinage d’urgence. ( 13 points )
Un véhicule roule en ligne droite sur une route horizontale à la vitesse de 72 km.h
-1
. Soudain, le conducteur
aperçoit un obstacle sur la route. Il actionne les freins et s’arrête.
1. Montrer que la vitesse de déplacement du véhicule avant le freinage vaut 20 m.s
-1
.
2. L’énergie cinétique d’un système en mouvement de translation est donnée par la relation
E
c
= 1
2 m v
2
.
2.1 Préciser les noms et unités légales de chaque grandeur présente dans la relation précédente.
Déterminer l’énergie cinétique Ec
1
du véhicule avant le freinage. Donnée : m
véhicule
= 1000 kg
2.2 Déterminer l’énergie cinétique du véhicule Ec
2
lorsqu’il est à l’arrêt.
2.3 En déduire la variation de l’énergie cinétique du véhicule pendant la phase de freinage.
3. Pendant la phase de freinage, seule la force due aux freins travaille. L’expression de son travail est
W
AB
F = –3600 x d
F
où d
F
est la distance parcourue pendant le freinage.
3.1 Justifier le signe moins dans l’expression du travail de la force
de freinage.
3.2 En appliquant le théorème de l’énergie cinétique, calculer la
distance de freinage d
F
.
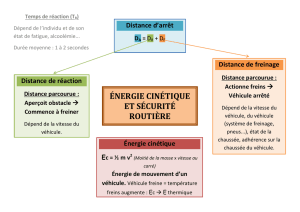
4. Un ordinateur portable de masse m = 5 kg était posé sur la
plage arrière du véhicule. N’étant pas attaché, il ne va pas
subir le freinage du véhicule et continue son mouvement
rectiligne avec la vitesse de 20m.s
-1
. Son énergie cinétique est
de 1200 J. Il vient frapper le conducteur. En exploitant la
courbe ci contre qui indique l’énergie cinétique au sol d’un
objet de masse m = 50 kg qui tombe en fonction de l’altitude de départ, conclure quant au danger de laisser
un objet posé sur la plage arrière d’un véhicule en mouvement.
Classe de TSTS
3
Devoir n° 9 28 mai 2014
P
F
R
N
f
Ec
en J
h en m