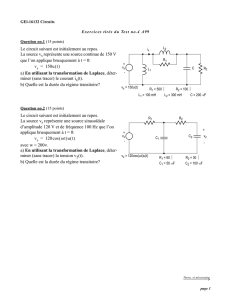
Transformée de Laplace

Transform´ee de Laplace
Automne 2016
1 Transform´ee de Laplace
On a souvent des probl`emes qui d´emarrent `a t= 0 et ´evoluent `a partir de conditions initiales
dans ces cas l`a, la transform´ee de Fourier n’est pas adapt´ee.
On va consid´erer une autre transformation plus adapt´ee `a cette situation qui partage de nom-
breuses propri´et´es avec la transform´ee de Fourier : La transform´ee de Laplace. On retrouve le calcul
symbolique de l’ing´enieur Heaviside.
2 Int´egrale de Laplace formelle
La variable t, dans tout ce qui suit, sera r´eelle, et on la supposera positive (elle repr´esentera
souvent le temps).
On fait correspondre `a une fonction fde la variable t, une fonction Lfd’une nouvelle variable
ppar la formule
Lf(p) = Z∞
0
e−ptf(t)dt (1)
La variable psera g´en´eralement complexe, on posera p=x+iy. Si l’int´egrale pr´ec´edente est
d´efinie, Lfs’appelle la transform´ee de Laplace de f.
On ne peut pas calculer la transform´ee de Laplace de n’importe quelle fonction f.
On supposera que
1. fest nulle sur R−∗ (c’est une convention, dont l’utilit´e apparaˆıtra plus tard), une telle
fonction est appel´ee causale,
2. fest continue par morceaux sur R+,
3. il existe une constante Mpositive telle que le produit
e−Mt|f(t)|
reste born´e pour toutes les valeurs de tassez grandes (i.e. pour t>t0avec t0∈R+,t0
d´ependant de Met de f).
La derni`ere condition signifie que fest d’ordre exponentiel M:
D´efinition 2.1. Une fonction ftelle que
|f(t)|6CeMt,pour tout t≥t0
avec C∈R+, est dite d’ordre exponentiel M.
1

Cette condition est suffisante pour que l’int´egrale 1 soit d´efinie pour toutes les valeurs de
p=x+iy telles que x>M.
Th´eor`eme 2.2. Si fest une fonction continue par morceaux sur R+, et d’ordre exponentiel M,
alors, ∀p∈Ctel que Re(p)> M, l’int´egrale (1) est bien d´efinie.
On appelle abscisse de convergence le r´eel
pf= inf{r∈R;t7→ f(t) exp(−rt) est int´egrable sur R+}.
Si pf<+∞, alors Lf(p) est bien d´efinie pour Re(p)> pf.
pf
Si fest d’ordre exponentiel Malors pf≤M.
Consid´erons deux fonctions fet gtelles que l’on puisse d´efinir leur transform´ee de Laplace,
pour Re(p)> pfpour fet Re(p)> pgpour g. Alors, nous avons
∀(a, b)∈C,L{af +bg}(p) = aLf(p) + bLg(p)
pour tout ptel que Re(p)>max(pf, pg).
Soit fune fonction admettant une transform´e de Laplace, et kune constante positive. Si on
change l’´echelle dans fen cr´eant la nouvelle fonction e f(t) = f(kt), alors
Le f(p) = 1
kLfp k,
pour Re(p)> kpf.
La d´emonstration est imm´ediate en utilisant le changement de variables u=kt.
Si Lf(p) est la transform´ee de Laplace de f(t), alors
Lf(p+a)=L{e−atf(t)}(p),
pour Re(p+a)> pf.
En effet : L{e−atf(t)}(p) = R∞
0e−(a+p)tf(t)dt = Lf(p+a), `a condition que Lf(p+a) soit
d´efinie.
Exercice 2.3. Calculer
L{e3tsin(2t)}(p).
2

Soit h > 0, alors :
L{f(t−h)}=e−phLf(p),
pour Re(p)> pf.
En effet, ayant suppos´e que fest nulle sur R−∗ , on a f(t−h) = 0 pour t<h:
L{f(t−h}(p) = Z∞
0
e−ptf(t−h)dt
=e−ph Z∞
h
e−p(t−h)f(t−h)dt
=e−ph Z∞
0
e−puf(u)du.
Le th´eor`eme suivant est fondamental dans la th´eorie du calcul symbolique.
Th´eor`eme 2.4. Si fest une fonction de classe C1sur R+, si elle est d’ordre exponentiel Met si
f0admet une transform´ee de Laplace, alors
L{f0}(p) = pLf(p)−f(0),
pour Re(p)> M.
Si l’on applique plusieurs fois la r`egle pr´ec´edente, on trouve, si fest de classe C2, et f, f0d’ordre
exponentiel M:
L{f00}(p) = p2Lf(p)−pf(0) −f0(0),
et plus g´en´eralement, si fest de classe Cnet f, f0, . . . , fn−1d’ordre exponentiel M:
L{fn}(p) = pnLf(p)−pn−1f(0) −pn−2f0(0) −. . . −f(n−1)(0).
Remarques 2.5.1. Une fonction fpeut avoir une transform´ee de Laplace, sans que sa d´eriv´ee
f0en ait une.
exemple : f(t) = t−1/2a une transform´ee de Laplace valant pπ/p, mais f0(t) n’a pas de
transform´ee de Laplace, car pour cette fonction, l’int´egrale de Laplace diverge en 0.
2. La transformation de Laplace fait correspondre `a la d´erivation par rapport `a tla multiplica-
tion de la transform´ee de Laplace par p, avec l’addition d’une constante. C’est la simplicit´e
de cette r`egle qui explique l’emploi du calcul symbolique.
Exercice 2.6. Trouver la transform´ee de Laplace de ylorsque yest solution du probl`eme initial
d2y
dt2−7dy dt + 12y= 16e2t
y(0) = 6
dy
dt (0) = 4
Proposition 2.7. Soit fune fonction continue sur R+admettant une transform´ee de Laplace. Si
F(t)est une primitive de f(t), nulle pour t= 0, admettant une transform´ee de Laplace, on a :
LF(p) = 1
pLf(p).
3

C’est une cons´equence imm´ediate du th´eor`eme pr´ec´edent. On peut ´ecrire
LZt
0
f(u)du(p) = 1
pLf(p)
et en appliquant nfois cette r`egle :
LZt
0Ztn−1 0
. . . Zt1
0
f(u)dudt1. . . dtn−1(p) = 1
pnLf(p).
Exercice 2.8. Soit f(t) = tn, avec n∈N. Montrer que
Lf(p) = n!
pn+1 ,si Re(p)>0.
Exercice 2.9. Soit f(t) = eat, avec a∈R. Montrer que
Lf(p) = 1
p−a,si Re(p)> a.
Exercice 2.10. Montrer que, si f(t) = eiat, avec a∈R, nous avons
Lf(p) = 1
p−ia,si Re(p)>0.
Exercice 2.11. Montrer que les transform´ees de Laplace des fonctions cos(ωt) et sin(ωt), pour
tout ωr´eel, sont donn´ees par
L{cos(ωt)}(p) = p
p2+ω2,si Re(p)>0.
et
L{sin(ωt)}(p) = ω
p2+ω2,si Re(p)>0.
Exercice 2.12. Pour tout br´eel, on a
L{ch(bt)}(p) = p
p2−b2,si Re(p)>|b|.
et
L{sh(bt)}(p) = b
p2−b2,si Re(p)>|b|.
Maintenant, on d´esire calculer
L{tα}(p) = Z∞
0
e−pttαdt, p > 0
avec α∈]−1; +∞[ (pour assurer la convergence de l’int´egrale).
Posons u=tp. Alors, par changement de variables, nous avons
L{tα}(p) = 1
pα+1 Z∞
0
e−uuαdu
pour p > 0 et α > −1. La derni`ere int´egrale est ind´ependante de p, on peut donc poser
L{tα}(p) = cα
pα+1
4

o`u
cα=Z∞
0
e−uuαdu
Introduisons la fonction Γ d´efinie par
Γ(x) = Z∞
0
e−uux−1du.
Alors, cα= Γ(α+ 1), ce qui implique que
L{tα}(p) = Γ (α+ 1)
pα+1 , p > 0.
On peut montrer que la fonction Γ, bien connue dans le domaine des math´ematiques, est telle que
Γ1
2=√π
et
Γ (x+ 1) = xΓ (x), x > 0.
Consid´erons enfin la fonction de Heaviside Het prenons la translat´ee de cette fonction par a:
H(t−a), telle que
ua(t) = 0,si t<a
1,si t≥a
Alors, nous en d´eduisons que
L{ua(t)}(p) = Z∞
0
e−ptua(t)dt
En d´ecoupant le calcul entre [0; a] et [a;∞], on obtient, si Re(p)>0,
L{ua(t)}(p) = 1
pe−ap, a ≥0.
3 D´erivation et transform´ee de Laplace
Th´eor`eme 3.1. Soit ϕ=L{f}, o`u fest une fonction continue par morceaux d’ordre exponentiel
M. Alors ϕ(p)est diff´erentiable en tout ptel que Re(p)> M et
L{tf (t)}(p) = −dϕ
dp
Remarque 3.2.On a d´emontr´e le th´eor`eme dans le cas p∈R. Le cas p∈Cdemande d’avoir eu le
cours sur la d´erivation des fonctions complexes qui va suivre.
Proposition 3.3. Soit ϕ=L{f}, o`u fest une fonction continue par morceaux d’ordre exponentiel
M. Alors ϕ(p)est infiniment diff´erentiable pour ptel que Re(p)> M et
L{tnf(t)}(p)=(−1)ndnϕ
dpn, n = 1,2, ...
5