Quantiles Fichier

PRF α
]0,1[ α P ν
P(] − ∞, ν]) ≥α P ([ν, +∞[) ≥1−α,
F(ν)≥α F (ν−)≤α.
X(Ω,F, P )
F α ∈]0,1[ X α PX
α X ν
F(ν)≥α F (ν−)≤α P (X≤ν)≥α P (X≥ν)≥1−α
F−1(α) = {θ}θ α
F−1(α)=[a, b[F−1(α)=[a, b]a < b α
[a, b]

F−1(α) = ∅θ= inf{t∈R:F(t)≥α}α
X h α X θ
Rθ
−∞ h(x)dx =αR+∞ θh(x)dx = 1 −α
1/2.
1/4
3/4
ie1≤i≤9i/10
ie1≤i≤19 i/20
ie1≤i≤99 i/100
α
[a, b]a < b
α(a+b)/2
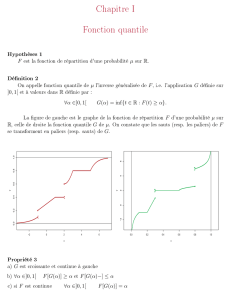
F X
Mα X x y
Mx < y z ∈]x, y[F(z)≥F(x)≥α F (z−)≤F(y−)≤α
zM M
I−={x∈R:F(x)≥α}[a, +∞[a∈R
I−F
I−lim
t→+∞F(t) = 1
I−lim
t→−∞F(t) = 0
I−I−F
x∈]−∞, a[I−a= inf{t∈R:F(x)≥α}F(x)< α
F(a−)≤α a α
I+={x∈R:F(x−)≤α}]− ∞, b]
b∈R
x→F(x−)

b α
M= [a, b]
F X
X F G ]0,1[
R
∀α∈]0,1[ G(α) = inf{t∈R:F(t)≥α}.
α∈]0,1[ G(α)
α F −1(α) = [a, b[F−1(α) = [a, b]a < b
G(α) = a
quantile(x, α, type = 1) α
a α [a, b]quantile(x, type = 1)
quantile(x, α, type = 2) α
a+b
2α[a, b]quantile(x, type =
2)
Q1
Q3
1re
D1
D9
boxplot a
a Q1−1,5(Q3−
Q1)a Q3+ 1,5(Q3−Q1)
[Q1−∆, Q3+ ∆] ∆ = 1,5(Q3−Q1)

(x1, n1), ..., (xk, nk)N=Pk
i=1 nkfi=ni/N
F P =Pk
i=1 fiδxi=1
nPk
i=1 niδxi
F
x∈]− ∞, x1[F(x) = 0
x∈[xk,+∞[F(x) = 1
x∈[xi, xi+1[F(x) = Fii= 1, ..., k −1
F(x1, n1), ..., (xk, nk)
α∈]0,1[
i F (xi) = α α
[xi, xi+1]
α xiF(xi−1)< α < F (xi)
f(x) = Pk
i=1 ni|x−xi|
x1≤x2≤... ≤xn
α∈]0,1[
nα /∈Nα x[nα]+1 [nα]nα
nα =q∈Nα[xq, xq+1]
nα =q∈Nα
xq+xq+1
2xq
x1≤... ≤x1≤x2≤... ≤x2≤... ≤xkxini

105/10 = 10,5D1= 15
105/4 = 26,25 Q1= 20
105/2 = 52,5µ= 20
3
4105 = 78,75 Q3= 30
9
10105 = 94,5D9= 35
F
[a0, a1[ [a1, a2[ [ap−1, ap[
n1n2np
F P =Pp
i=1 fiUai−1,aiUa,b
[a, b]
F
x∈]− ∞, a0]F(x)=0
x∈[ap,+∞[F(x) = 1
F(ai) = Fii= 1, ..., p −1Fi=Pi
k=1 fkie
F
[a0, a1[ [a1, a2[ [ap−1, ap[
n1n2np
α∈]0,1[ α ν F (ν) = α
α F −1({α}).