genetique des populations

Par Krys3000 (Groupe « The Trust » - http://www.cours-en-ligne.tk/) Page 1
GENETIQUE DES POPULATIONS
CHAPITRE IV : LA DERIVE GENETIQUE
I – DEFINITIONS
Dans une population naturelle, l’effectif n’est jamais infini. Analysons donc l’impact de l’effectif d’une population sur sa
constitution génétique et sur la variation des fréquences alléliques dans le temps. On peut étudier pour cela des populations
insulaires ou isolées.
Afin de simplifier considérons une population idéale, c’est-à-dire panmictique, d’effectif N constant et sans mutation, sélection
ou migration. Pour chaque locus autosomique, si on a 2 allèles, au final à la génération suivante, on aura 2N allèles tirés au
hasard représentant un échantillon des allèles des parents. Les fréquences alléliques ne sont alors pas forcément identiques à la
génération d’avant, l’échantillonnage pouvant provoquer une variation aléatoire des fréquences : c’est la dérive génétique.
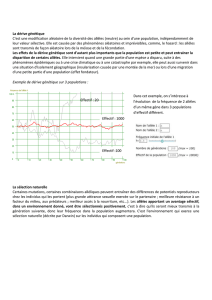
Sur une population de 40 individus avec f(A) = 0.75 et f(a) = 0.25, pour conserver ses valeurs à la génération suivante sachant
qu’on va impliquer 80 gamètes, il faut donc 60 A et 20 a. La probabilité que ce soit le cas est de :
P =
଼଴!
଺଴! ∗ ଶ଴!
∗ 0.75
60
∗ 0.25
20
= 0.103
Soit uniquement 10 %. Dans le reste des cas, il y a eu dérive. Comme la population est panmictique, les fréquences génotypiques
sont généralement proches des proportions de Hardy-Weinberg, et différent par le simple effet du hasard de l’échantillonnage.
On a ici deux urnes gamétiques, une pour chaque parent, considérées de même contenu. La composition des urnes ne dépend
que des parents la constituant, pas des urnes antérieures. Il y aura donc, à la génération suivante, un nouveau tirage aléatoire,
toujours régi par une loi binomiale (avec deux paramètres : p et 2N) mais ceux-ci auront des valeurs différentes. Cela permet
d’établir par ordinateur une simulation d’évolution dans une population d’effectif limité.
II – FIXATIONS
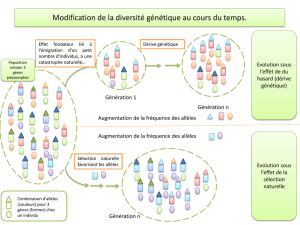
A terme, la dérive génétique entraine vers la fixation d’un allèle, dont la fréquence atteint 1 ; la population est alors totalement
homozygote. L’effet de la dérive est d’autant plus important que la population est faible (vu que si elle est infinie, on est en
condition de HW). La dérive homogénéise donc les populations. Seule, elle entraîne à terme l’homozygotie obligatoire.
Même si les croisements se font au hasard, le fait que la population soit d’effectif limité implique que la probabilité d’une union
entre individus apparentés existe  on à augmentation de la consanguinité.
On peut calculer la probabilité de fixation d’un allèle, même si on ne peut pas prédire le devenir d’une population en particulier
(car le processus est stochastique c'est-à-dire aléatoire). Cette probabilité dépend de sa fréquence dans la population ; le
processus étant aléatoire, si sa fréquence est de 0.9, il aura 90 chances sur 100 d’être fixé, 10 chances d’être éliminé.
Dans une population totalement isolée, idéale, on peut s’apercevoir, par analyse, que tous les gènes finiront par provenir d’un
seul gène ancêtre : c’est la coalescence, un phénomène de fixation mais vers le passé au lieu du futur  confirmation de
l’augmentation de la consanguinité au cours du temps, car on a de plus en plus de chance de tirer deux gènes identiques.