Cosinus d`un angle aigu

Cosinus d’un angle aigu
I) Définitions :
a) Côté adjacent et hypoténuse :
Définition n°1 :
Dans un triangle rectangle :
• l’hypoténuse est le côté opposé à l’angle droit (c’est le plus long des trois côtés)
• le côté adjacent à un angle aigu est le côté de cet angle qui n’est pas
l’hypoténuse.
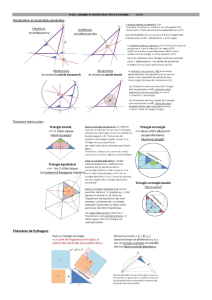
Exemple :
Soit ABC un triangle rectangle en B :
Angle
On repère ses côtés : [AB] et [AC].
Comme [AC] est l’hypoténuse, on en
déduit que [AB] est la côté adjacent à
l’angle .
Angle
On repère ses côtés : [CA] et [CB].
Comme [CA] est l’hypoténuse, on en
déduit que [CB] est la côté adjacent à
l’angle .

Remarque :
On rappelle que les angles aigus d’un triangle rectangle sont complémentaires, c’est-
à-dire deux angles dont la somme des mesures fait 90°.
Dans le triangle précédent, les angles 
 et   sont complémentaires, on peut
donc écrire que :
 +   = 90
Par exemple, si 
 = 36°, on en déduit que   = 90 –   = 90 – 36 = 54°.
Définition n°2 :
Dans un triangle rectangle, le cosinus d’un angle aigu est égal au quotient de la
longueur du côté adjacent à cet angle par la longueur de l’hypoténuse.
Exemple :
Le triangle DEF est rectangle en D. Ecrire la formule donnant le cosinus de l’angle aigu
.
On commence par faire une figure pour visualiser la situation :
On repère le côté adjacent de l’angle 
 et l’hypoténuse :

Puis on écrit la formule et on remplace par les bonnes données :
Cos(
) = 
Cos(
) = 
Conclusion : Cos(
) = 
Remarque :
Comme la longueur du côté adjacent est strictement inférieure à la longueur de
l’hypoténuse, le cosinus d’un angle est toujours compris entre 0 et 1.
II) Calcul d’une longueur :
a) Calcul de la longueur du côté adjacent :
Exemple :
Soit ABC un triangle rectangle en A tel que BC = 5 cm et 
 = 50°.
Déterminer la longueur du côté [AB] arrondie au dixième.
Méthode :
Première étape : construire une figure à main levée où on repère l’hypoténuse et le
côté adjacent à l’angle donné 
.

Deuxième étape : on écrit le cosinus d’un angle : la longueur cherchée doit apparaître
dans le quotient :
Cos(
) =  !"
Cos(
) =
!
!"
Troisième étape : on remplace ce que l’on peut par les données de l’énoncé :
Cos(50) =
!
#
( on a remplacé 
 par 50 et BC par 5 )
Quatrième étape : on écrit l’égalité précédente sous forme d’une égalité de quotients :
"$#%&
'
=
!
#
=> on pourra ainsi appliquer la quatrième proportionnelle.
Cinquième étape : on applique la quatrième proportionnelle pour calculer AB :
AB =
#("$#%&
'
AB ) 3,2 cm, valeur arrondie au dixième.
Conclusion : AB ) 3,2 cm
b) Calcul de la longueur de l’hypoténuse :
Exemple :
Soit ABC un triangle rectangle en B tel que AB = 8 m et 
 = 34°.
Déterminer la longueur du côté [AC] arrondie au dixième.

Méthode :
Première étape : construire une figure à main levée où on repère l’hypoténuse et le
côté adjacent à l’angle donné 
.
Deuxième étape : on écrit le cosinus d’un angle : la longueur cherchée doit apparaître
dans le quotient :
Cos(
) = ! "
Cos(
) =
!
"
Troisième étape : on remplace ce que l’on peut par les données de l’énoncé :
Cos(34) =
*
"
( on a remplacé 
 par 34 et AB par 8 )
Quatrième étape : on écrit l’égalité précédente sous forme d’une égalité de quotients :
"$+,&
'
=
*
"
=> on pourra ainsi appliquer la quatrième proportionnelle.
Cinquième étape : on applique la quatrième proportionnelle pour calculer AC :
AC =
*('
"$+,&
AC ) 9,6 m, valeur arrondie au dixième.
Conclusion : AC ) 9,6 m