PHY244_CC mars_2013-2014

1
UE PHY244 – Vibrations, ondes et optique ondulatoire, 2013-2014
L2 Université Joseph Fourier, Grenoble
UE PHY244 - Examen partiel du 19 mars 2014 – durée 2h – 6 pages
Calculatrice interdite, documents interdits, téléphone portable interdit
Le barème approximatif (sur 20,5) est noté entre parenthèses et est donné à titre indicatif.
Le sujet paraît long mais la plupart des questions attendent une réponse courte. On veillera à répondre de
façon précise et concise.
Le sujet comporte de nombreuses questions indépendantes. Il ne faut donc pas rester bloqué(e) sur une
question.
On peut en particulier traiter les questions A.4. et toutes les questions de la partie B dans l’ordre de son
choix. A l’intérieur d’une même partie, certaines questions peuvent être traitées indépendamment.
Les calculs numériques sont prévus pour être réalisés sans calculatrice. Un résultat numérique donné
sans unité ne sera pas pris en compte.
A. SYSTEME DE MASSES LIEES PAR UN OU PLUSIEURS RESSORTS
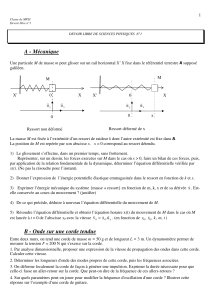
Sur un axe vertical fixe Oz peuvent coulisser deux petits cylindres assimilables à deux masses ponctuelles m
et m’, reliées par un ressort de raideur k, de masse négligeable et de longueur au repos κ
଴
.
A l’équilibre, la masse m’ est en contact avec un support horizontal fixe et le ressort a pour longueur κ
±௤
(figure 1). A un instant t quelconque, on note κ la longueur du ressort.
On note ݃Ԧ l’accélération de la pesanteur et ݑ
௭
ሬ
ሬ
ሬ
ሬ
Ԧ
le vecteur unitaire (vertical orienté vers le haut).
1. (3,5 points)
1.1. Donner l’expression de la force exercée par le ressort sur la masse m quand le ressort à pour
longueur κ (on demande une relation vectorielle).
1.2. Déterminer la longueur κ
±௤
du ressort à l’équilibre.
On abaisse la masse m en comprimant le ressort jusqu’à la longueur κ
ଵ
(κ
ଵ
< κ
±௤
) et on abandonne le
système sans vitesse initiale.
κ
±
௤
κ
଴
κ
ଵ
κ
ݑ
௭
ሬ
ሬ
ሬ
ሬ
Ԧ
figure 1

2
1.3. On suppose que la masse m’ reste sur le sol. On note z = κ െ κ
±௤
le déplacement de m par rapport
à la position d’équilibre. Montrer que z vérifie l’équation différentielle d’un oscillateur harmonique
et donner l’expression de la pulsation ߱
଴
de cet oscillateur.
1.4. En déduire l’équation du mouvement z(t) (on donnera la forme générale puis la solution
correspondant aux conditions initiales).
1.5. a) En déduire l’expression de la force exercée ܨ
ᇱ
ሺݐሻ
ሬ
ሬ
ሬ
ሬ
ሬ
ሬ
ሬ
ሬ
ሬ
ሬ
Ԧ
par le ressort sur la masse m’ au cours du
temps (on demande une relation vectorielle).
b) En déduire la valeur ܨ
௠௔௫
ᇱ
que prend le module de ܨ
ᇱ
ሺݐሻ
ሬ
ሬ
ሬ
ሬ
ሬ
ሬ
ሬ
ሬ
ሬ
ሬ
Ԧ
.
1.6. Si on comprime fortement le ressort initialement, on pourra faire décoller la masse m’ du plan
horizontal.
Exprimer, en la justifiant, la condition portant sur κ
ଵ
pour que m’ puisse se soulever (on exprimera
la condition en fonction des données : κ
଴
, κ
ଵ
, m, m’, g et k).
Dans ce qui suit, on suppose que la masse m’ ne décolle pas et reste en permanence sur le plan horizontal.
2. (1,5 point)
On plonge tout le système (y compris le plan horizontal qui supporte m’ ) dans une éprouvette remplie
d’un fluide visqueux qui introduit une force de frottement proportionnelle et opposée à la vitesse ݒԦ de m :
݂ሺݐሻ
ሬ
ሬ
ሬ
ሬ
ሬ
ሬ
ሬ
ሬ
Ԧ
ൌ  െߙݒԦ .
2.1. Donner, sans démonstration, la nouvelle forme que prend l’équation différentielle du mouvement
vérifiée par z = κ െ κ
±௤
.
2.2. Quelle inégalité doit vérifier le coefficient de frottement ߙpour que le mouvement de m soit
pseudopériodique (mouvement oscillatoire amorti) ?
2.3. a) Dans l’hypothèse du mouvement pseudopériodique, donner la forme générale de l’équation du
mouvement z(t) (on se limitera à la forme générale sans tenir compte des conditions initiales).
b) Donner la valeur de la pseudo-pulsation ߱
௣
et de la pseudo-période ܶ
௣
en fonction des données
de l’énoncé.
3. (2 points)
On reprend le matériel initial sans amortissement (c’est-à-dire sans
l’éprouvette avec le fluide visqueux).
On place cette fois-ci l’ensemble ሼ݉ ൅  ൅ ݉ǯሽsur
un autre ressort reposant directement sur un vibreur (figure 2). On obtient
donc un système de deux oscillateurs couplés.
On fait en sorte que tous les déplacements soient verticaux et on impose
au vibreur un mouvement vertical sinusoïdal de fréquence f .
On ne s’intéresse qu’au résultat obtenu en régime sinusoïdal permanent.
3.1. Donner la définition de l’expression « régime sinusoïdal
permanent ».
3.2. a) Donner (sans démonstration) l’allure des deux courbes
représentant l’évolution des amplitudes des mouvements
d’oscillations forcées des deux masses m et m’ en fonction de
la fréquence (on soignera le tracé).
vibreur
figure 2

3
b) Préciser à quoi correspondent les fréquences remarquables sur les courbes (sans chercher à
donner leur expression).
c) Donner le nom des phénomènes physiques remarquables qui apparaissent sur ces courbes
pour certaines fréquences.
4. (2,5 points)
On considère maintenant un système d’oscillateurs couplés constitué de 3 masses identiques m reliées
entre elles et aux extrémités fixes (à droite et à gauche) par des ressorts identiques de raideur k (figure 3).
On suppose que les masses se déplacent horizontalement (le poids étant compensé par la réaction d’un
support qui n’est pas représenté).
figure 3
(les flèches indiquent les déplacements
ݔ
ଵ
ǡ ݔ
ଶ
et ݔ
ଷ
par rapport aux positions d’équilibre)
4.1. Donner la définition d’un mode propre.
4.2. Combien y-aura-t-il de modes propres ?
4.3. Sans faire de calcul, préciser les conditions initiales qui peuvent donner lieu à une oscillation dans
l’un des modes propres – on pourra s’aider d’un simple schéma pour traduire les conditions
initiales de chacune des situations envisagées (on ne traitera pas le cas de tous les modes propres
mais on se limitera aux situations les plus évidentes intuitivement).
4.4. Si ݔ
ଵ
ሺݐሻ désigne le déplacement suivant Ox de la première masse par rapport à sa position
d’équilibre, donner la forme la plus générale de ݔ
ଵ
ሺݐሻ en régime libre.
4.5. Représenter l’allure du spectre en fréquence deݔ
ଵ
ሺݐሻ dans le cas le plus général.
B. ONDE SUR UNE CORDE, ONDE SONORE, ONDE DANS UN CABLE COAXIAL
On s’intéresse aux ondes dans différents milieux.
1 à 4. (2 points)
1. Rappeler l’équation d’onde de d’Alembert à une dimension satisfaite par une onde représentée par
une fonction y(x,t).
2. Quelle est la forme la plus générale de la solution de cette équation ?
3. Quelle est la forme la plus générale d’une onde progressive se propageant dans le sens des x
croissants ?
Pour la corde, on s’intéressera au déplacement vertical y(x,t) d’un point à l’abscisse x.
k
k
k
k m
x
1
x
2
x
3
m
m

4
Pour le câble coaxial, à la tension V(x,t) entre le fil central et le blindage du câble à l’abscisse x (figure 4).
figure 4 : câble coaxial
Pour l’onde sonore, on s’intéresse à la surpression p(x,t) et à la vitesse v(x,t) de déplacement des molécules.
4. Donner un ordre de grandeur des célérités de l’onde :
a) pour la corde
b) pour le câble
c) pour une onde sonore dans l’air, dans l’eau et dans un métal.
5. Propagation d’une déformation sur une corde (2,5 points)
Au repos, la corde est horizontale (figure 5). La poulie relie la corde à une masse M dont le poids
permet de régler la tension T de la corde.
figure 5
On considère que le point A (situé au niveau de la poulie sur la figure 5) est fixe et constitue l’extrémité
droite de la corde.
On donne OA = L = 5 m.
5.1. Calculer la valeur de la célérité c de la propagation, sachant que la tension vaut T = 1 N et que la
masse linéique de la corde vaut µ = 40 g/m (en cas d’oubli, on pourra retrouver la relation entre c,
T et µ à partir d’une analyse dimensionnelle).
5.2. On fait subir au point O (extrémité gauche) une déformation dissymétrique de courte durée de la
forme ݕ
௜
ሺͲǡ ݐሻ suivante (figure 6).
figure 6
Représenter l’allure de la corde à l’instant ݐ
ଷ
ൌ Ͳǡ͸s : ݕ
௜
ሺݔǡ ݐ
ଷ
ሻ (on précisera les valeurs de x
remarquables).
ݐ
ଶ
ൌ
Ͳ
ǡ
ͷ
s
ݐ
ଵ
ൌ
Ͳ
ǡ
ͳ
s
ݕ
௜
ሺ
Ͳ
ǡ
ݐ
ሻ
0
t
A O
poulie
M

5
5.3. Au bout de combien de temps (ݐ ൌ ݐ
஺
) la perturbation atteint-elle l’extrémité A ?
5.4. La déformation va subir une réflexion sur l’extrémité A supposée fixe. On note ݕ
௥
ሺݔǡ ݐሻ l’onde
réfléchie.
a) Comment s’exprime la condition aux limites satisfaite par les ondes ݕ
௜
et ݕ
௥
à l’extrémité A ?
b) Représenter l’allure de la corde quand, après réflexion sur l’extrémité A, la perturbation
réfléchie a atteint le milieu de la corde (on ne demande ni calcul ni justification mais il faut
prendre en compte la dissymétrie de la perturbation).
5.5. Analogie avec les ondes dans un câble ou le son : quelle est la situation qui correspond à la
condition aux limites envisagée ici (extrémité fixe de la corde) :
a) pour la tension V(x,t) dans le cas du câble coaxial : court-circuit, circuit ouvert, résistance de
valeur particulière ?
b) pour la surpression p(x,t) dans le cas d’un tuyau sonore : tuyau fermé, tuyau ouvert, forme
particulière de l’extrémité du tuyau (exemples : extrémité d’un porte-voix, extrémité d’une
trompette) ?
6. Onde sonore sinusoïdale (4 points)
Un haut-parleur situé en un point O émet un son sinusoïdal de fréquence f.
On considère que la surpression de l’onde sonore p(x,t) est bien représentée par une onde progressive
d’amplitude ݌
௠
se propageant dans le sens des x croissants avec une célérité c. On note ߩ
଴
la masse
volumique de l’air.
6.1. Que vaut la longueur d’onde ߣ pour f = 1 kHz (expression littérale puis valeur numérique) ?
6.2. Donner l’expression littérale (sans valeurs numériques) de p(x,t) utilisant la période T et la
longueur d’ondeߣ et en supposant que p(0,0) = ݌
௠
(valeur à l’instant initial t = 0 en x = 0).
6.3. En déduire l’expression de la vitesse des particules v(x,t) (expression littérale seulement, en
fonction des données de l’énoncé).
6.4. Un son soutenu, d’intensité acoustique ܫ
ௗ
= 2 W/m², est douloureux.
L’intensité acoustique ܫ
௔௖
est la puissance moyenne transmise par l’onde par unité de surface.
Démontrer la relation qui lie l’intensité acoustique en un point (dans l’hypothèse d’un son
sinusoïdal) :
a) à l’amplitude ݌
௠
de la surpression
b) à l’amplitude ݒ
௠
de la vitesse
6.5. Calculer l’ordre de grandeur de ݒ
ௗ
, valeur de ݒ
௠
correspondant à ܫ
ௗ
= 2 W/m² (pour cela, on
considérera que, très approximativement, ܿ ؄ ͶͲͲm/s et ߩ
଴
؄ ͳ kg/݉
ଷ
) .
6.6. Toujours pour une onde sinusoïdale de fréquence f, quelle est la relation entre l’amplitude ݒ
௠
de la
vitesse et l’amplitude ݔ
௠
du déplacement.
6.7. En déduire la valeur numérique de l’amplitude ݔ
ௗ
du déplacement maximal des molécules d’air
correspondant à ܫ
ௗ
pour une fréquence f de l’ordre de 1 kHz (on prendra f = 1590 Hz §
ଵ଴
ଶగ
Ǥ ͳͲ
ଷ
Hz, ce qui permet de simplifier les calculs). On donnera le résultat dans une unité adaptée à l’ordre
de grandeur.
6.8. Définir le niveau d’intensité acoustique ܮ
ௗ஻
(on rappelle que le niveau de référence est ܫ
௠௜௡
ൌ
ͳͲ
ିଵଶ
W/m²). Quel est l’intérêt pratique d’utiliser cette grandeur ?