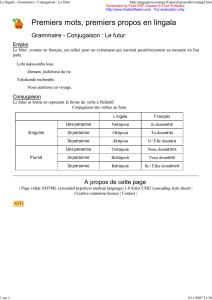
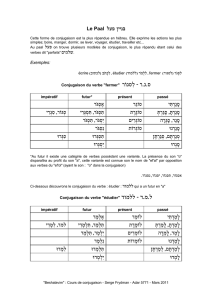
Année universitaire 2016/2017 Licence 2, S4, mathématiques

Ann´ee universitaire 2016/2017
Licence 2, S4, math´ematiques
Structures alg´ebriques 1 – Feuille 7
Exercice 1 (Th´eor`eme de Cauchy – cas ab´elien)
Dans cet exercice et l’exercice 5, on donne une preuve du th´eor`eme de Cauchy : si Gest un
groupe fini d’ordre divisible par ppremier alors Gcontient un ´el´ement d’ordre p.
Dans cet exercice on suppose que Gest ab´elien d’ordre nmultiple d’un nombre premier p.
(1) Pourquoi le th´eor`eme de Cauchy est-il ´evident si n=p? Dans la suite on suppose p<net
l’on suppose par l’absurde qu’aucun ´el´ement de Gn’est d’ordre p.
(2) Justifier qu’aucun ´el´ement de Gn’est d’ordre divisible par p. On note dans la suite g1,...,gn
les ´el´ements de G, et m1,...,mnleurs ordres respectifs.
(3) Posons m= ppcm(mi)i. Justifier que l’application f: (Z/mZ)n→Gd´efinie par f(a1, . . . , an) =
ga1
1· · · gan
nest un morphisme de groupes.
(4) En appliquant le th´eor`eme de factorisation, d´eduire une contradiction.
Exercice 2
Soit Gun groupe.
(1) Montrer que l’application G×G→Gd´efinie par (g, x)7→ gxg−1d´efinit une action de Gsur
lui-mˆeme (on l’appelle action par conjugaison ; une orbite pour cette action est une classe
de conjugaison de G).
On suppose qu’il existe une classe de conjugaison Cde Gtelle que Ca exactement 2 ´el´ements.
(2) Justifier que |G| ≥ 3. Le groupe Gest-il ab´elien ?
(3) On note Sym(C) le groupe des permutations de l’ensemble C. Quel est l’ordre de Sym(C) ?
On note dans la suite ϕ:G→Sym(C) le morphisme de groupes d´efini par
g7→ (x7→ gxg−1).
(4) Justifier que ker ϕ6={1}et que ker ϕ6=G.
(5) En d´eduire que le groupe Gn’est pas simple.
Exercice 3
(1) Soit Gun groupe fini. Notons g1, . . . , gkun ensemble de repr´esentants pour les classes de
conjugaison (cf exercice 2) de Gde cardinal >1. En notant Z(gi) le stabilisateur de gipour
l’action de Gpar conjugaison (c’est le centralisateur de gi), montrer que
(?)|G|=|Z(G)|+
k
X
i=1
(G:Z(gi)) .
On appelle p-groupe un groupe fini dont l’ordre est une puissance d’un nombre premier p.
(2) Soit Gun p-groupe. En utilisant (?) montrer que le centre Z(G) de Gest non trivial.
(3) Soit Gun groupe. Rappeler pourquoi l’ensemble quotient G/Z(G) peut ˆetre muni d’une
structure de groupe, puis montrer que si G/Z(G) est un groupe cyclique alors Gest ab´elien.
(4) Soit pun nombre premier. Montrer que tout groupe d’ordre p2est ab´elien.
1

Exercice 4
(1) Soit n≥1 un entier. Montrer que le groupe G= GL(Rn) agit sur Rnvia l’application
(M, v)7→ M(v), M∈G,v∈Rn.
(2) Combien y a-t-il d’orbites pour cette action ?
(3) Soit M∈Gdont la matrice relativement `a la base canonique de Rnest triangulaire
sup´erieure avec des coefficients diagonaux tous distincts de 0 et 1. Quels sont les vecteurs
v∈Rntels que M∈Stab(v) ?
(4) Soit v∈Rn\ {0}et soit M∈G. Traduire en termes des sous-espaces propres de Mle fait
que M∈Stab(v).
Exercice 5 (Th´eor`eme de Cauchy – cas non ab´elien)
On reprend les notations de l’exercice 1 `a cela pr`es que l’on suppose maintenant Gnon ab´elien.
On va d´emontrer le th´eor`eme de Cauchy par r´ecurrence sur n≥p. L’´etape d’initialisation est
´evidente (pourquoi ?). On fait l’hypoth`ese de r´ecurrence (forte) et l’on se donne un groupe Gnon
ab´elien d’ordre ndivisible par un nombre premier p<n.
(1) Justifier qu’il suffit de travailler sous l’hypoth`ese : tout sous-groupe propre Hde Gest
d’indice divisible par p.
(2) En reprenant les notations de Ex. 3(1), justifier que p|(G:Z(gi)) pour tout i∈ {1, . . . , k},
puis conclure en utilisant l’´equation (?) de l’exercice 3.
Exercice 6
On note O2(R) le groupe des isom´etries de l’espace euclidien R2.
(1) Montrer que O2(R) agit sur le cercle unit´e Cde R2centr´e en l’origine. Quelles sont les
orbites pour cette action ?
(2) ´ Etant donn´e un point x∈C, d´ecrire Stab(x).
(3) Soit n≥1 un entier. On inscrit dans Cun polygˆone r´egulier Pn`a nsommets. Quel est le
stabilisateur de Pndans l’action de O2(R) sur l’ensemble des parties de C?
(4) Reprendre la question pr´ec´edente en rempla¸cant O2(R) par le sous-groupe SO2(R) constitu´e
des rotations du plan euclidien.
Exercice 7
(1) Montrer que tous les 5-cycles sont dans la mˆeme orbite pour l’action par conjugaison de S5
sur lui-mˆeme. Comment g´en´eraliser ce fait aux k-cyles de Sno`u les entiers 1 ≤k≤nsont
fix´es ?
(2) Montrer que A5agit transitivement par conjugaison sur l’ensemble de ses 3-cycles.
(3) Combien y a-t-il d’orbites dans l’action par conjugaison de A5sur l’ensemble de ses 5-cycles ?
Exercice 8 (Lemme de Burnside)
Soit Gun groupe fini agissant sur un ensemble fini X. Si g∈G, on note χ(g) le nombre de x∈X
tels que g·x=x.
(1) Montrer la formule de Burnside :
|G| × |{Orbites de Gsur X}| =X
g∈G
χ(g).
(2) On suppose que l’action de Gsur Xest transitive et que |X| ≥ 2. On note G0l’ensemble
des g∈Gtels que χ(g) = 0. Montrer que |G0|/|G| ≥ 1/|X|. [On pourra appliquer le lemme
de Burnside `a l’action de Gsur X et, pour un x∈Xfix´e, `a l’action de Stab(x) sur X\ {x}.]
2