EM2_Cours_Mouvement de Charges dans un Champ EM_Poly

C
CC
CH2
H2H2
H25
55
5 :
: :
: M
MM
Mouvement
ouvementouvement
ouvement d
dd
de charges
e chargese charges
e charges dans
dans dans
dans un
un un
un cham
chamcham
champ
p p
p (E, B)
(E, B) (E, B)
(E, B) –
––
– 1
1 1
1/3
/3/3
/3
Objectif
ObjectifObjectif
Objectif ?
??
?  Etudier le mouvement des charges dans les champs électromagnétiques
Beaucoup d’a
Beaucoup d’aBeaucoup d’a
Beaucoup d’applications
pplicationspplications
pplications :
::
:  Oscilloscope / TV / Accélérateur de particule / Cyclotron / Spectromètre de masse
I
II
I Ch
ChCh
Champ magnétiq
amp magnétiqamp magnétiq
amp magnétique
ueue
ue
I.1
I.1I.1
I.1 Source de champ magnétique
Source de champ magnétiqueSource de champ magnétique
Source de champ magnétique
Champ électrique : Généré par des charges électriques
Champ magnétique : Généré par des mouvements de charges
CHAMP MAGNETIQUE = CHAMP VECTORIEL (En tout point de l’espace, on définit un vecteur…)
Unité : Le Tesla (T)
Mesure : Teslamètre – Sonde à effet Hall (voir TP / DM)
I.2
I.2I.2
I.2 Exemples d’interaction
Exemples d’interactionExemples d’interaction
Exemples d’interaction
 Attraction des pôles opposés ?  Orientation des aimants dans le sens du champ
I.3
I.3I.3
I.3 Couplage électromagnétique
Couplage électromagnétiqueCouplage électromagnétique
Couplage électromagnétique
Courant
CourantCourant
Courant
Ex : Fil Ex : Bobine
 Expressions calculées l’année prochaine…
Aimant
AimantAimant
Aimant
Ex : Aimant droit
 Mouvement microscopique des électrons
(spin = rotation sur eux même ≈ bobine)
N
S
S
N
N
S
N
S
Répulsion
SUD
-
SUD
Attraction
SUD
-
NORD
Aimant Droit
S
SS
S
N
NN
N
Les champs électrique
E
et magnétique
B
sont couplés (Toute variation de l’un entraine
une variation de l’autre)   On parle de Champ électromagnétique
On parle de Champ électromagnétique On parle de Champ électromagnétique
On parle de Champ électromagnétique
(
)
,
E B
En électrostatique :
(Charges immobiles)
0
E C stte
B
=
=
En magnétostatique :
(Courants constants ou
aimants permanents)
0 E
B C stte
=
=
On peut cependant les étudier de manière indépendante dans 2 cas précis
:

II
IIII
II Force de Lorentz
Force de LorentzForce de Lorentz
Force de Lorentz
II.1
II.1II.1
II.1 Ex
ExEx
Expression
pressionpression
pression
Soit une particule de charge q dans un champ électromagnétique :
(
)
,
E B
Elle est soumise à la force de Lorentz :
elec magn
F f f
F qE qv B
= +
= + ∧
Rmq
RmqRmq
Rmq :
::
: Règle de la main droite pour la force électromagnétique
Puissance
PuissancePuissance
Puissance :
::
: Puissance de la force de Lorentz : on a toujours
magn
f qv B v
= ∧ ⊥
 ne travaille pas
Ainsi :
0
F
P F v qE v
= ⋅ = ⋅ +
La force élec
La force élecLa force élec
La force électrique
triquetrique
trique travaille
travaille travaille
travaille
La force magnétique ne travaille pas (fait tourner…)
La force magnétique ne travaille pas (fait tourner…)La force magnétique ne travaille pas (fait tourner…)
La force magnétique ne travaille pas (fait tourner…)
II.2
II.2II.2
II.2 Mouvement dans un
Mouvement dans un Mouvement dans un
Mouvement dans un champ électrique uniforme
champ électrique uniformechamp électrique uniforme
champ électrique uniforme
Soit une particule de charge q dans un champ électrostatique
0
E C stte
B
=
=
elec
F f qE
= =
La force est constante – à q donné – et joue un rôle équivalent à la force de gravitation (
q E m g
↔ )
))
)
Rmq : La force électrique travaille 
W qE dl
δ
= ⋅
peut être différent de 0 (à représenter sur le schéma)
Différents cas de figure possibles
Différents cas de figure possiblesDifférents cas de figure possibles
Différents cas de figure possibles :
::
:
II.3
II.3II.3
II.3 Mouvement dans un champ magnétique uniforme
Mouvement dans un champ magnétique uniformeMouvement dans un champ magnétique uniforme
Mouvement dans un champ magnétique uniforme
Soit une particule de charge q dans un champ magnétostatique
0 E
B C stte
=
=
magn
F f qv B
= = ∧
Rmq : La force magnétique ne travaille pas 
(
)
0
P qv B v
= ∧ ⋅ =
 La |vitesse| reste constante
Différents cas de figure possibles
Différents cas de figure possiblesDifférents cas de figure possibles
Différents cas de figure possibles :
::
:
qv
B
magn
f qv B
= ∧
Lampe
d’émission
E
A
U
UU
U
Accélération
Faisceau
Cathode
Anode
E v
Accélération
AccélérationAccélération
Accélération
Ex : Canon
à électron
 Trajectoire rectiligne (voir TP)
(Tube cathodique de TV / Oscillo / …)
Charge q
U
Plaques métalliques
Générateur
E
q < 0
q
>
0
E v
⊥
Déviation
Déviation Déviation
Déviation
/ Déflexion
/ Déflexion/ Déflexion
/ Déflexion
Ex
:
Plaques
 Trajectoire parabolique (voir TP)
(Déviation du faisceau d’un oscilloscope)
B v
Pas d’action
Pas d’actionPas d’action
Pas d’action :
: :
:
0
F qv B
= ∧ =
Ex
:
Aucun
 Aucune Action
 Trajectoire rectiligne (voir TP)
Charge
q
B
0
F qv B
= ∧ =
Charge q
B
f
B v
⊥
Déviation / Déflexion
Déviation / DéflexionDéviation / Déflexion
Déviation / Déflexion
Ex : Déviation
Magnétique
 Trajectoire circulaire (voir TP)
Exemples : Déviation du faisceau dans TV /
Spectromètre de masse / Cyclotron (voir TD)
C
CC
C
H2
H2H2
H2
5
55
5
–
––
–
EM
EM EM
EM
2
22
2
–
––
–
2/
2/ 2/
2/
3
33
3

CH2
CH2CH2
CH25
55
5 : Mouvement de charges dans un champ (E, B)
: Mouvement de charges dans un champ (E, B) : Mouvement de charges dans un champ (E, B)
: Mouvement de charges dans un champ (E, B) –
––
– 3
33
3/3
/3/3
/3
III
IIIIII
III Application à l’électrocinétique
Application à l’électrocinétiqueApplication à l’électrocinétique
Application à l’électrocinétique
III.1
III.1III.1
III.1 Milieux
Milieux Milieux
Milieux C
CC
Conducteur
onducteuronducteur
onducteurs
ss
s
Milieu conducteur :  Ions métalliques fixes +
 Electrons mobiles –
Origine du mouvement :  Electrons mis en mvt par le champ électrique
E
elec
f q E
⇒=
Modélisation des interactions Ions / Electrons :  Force de frottement fluide
m
f k v v
τ
⇒= − ⋅ = − ⋅
P
PP
PFD
FDFD
FD sur l’électron
sur l’électron sur l’électron
sur l’électron :
::
:
m d v m
m a q E v m v q E
d t
τ τ
= − ⋅ ⇔ + ⋅ =
Résolution
RésolutionRésolution
Résolution :
: :
:
0 lim 0
t t
q
v E V e v V e
m
τ τ
τ
− −
= ⋅ + ⋅ = + ⋅
III.2
III.2III.2
III.2 Loi d’Ohm locale
Loi d’Ohm localeLoi d’Ohm locale
Loi d’Ohm locale
a)
a) a)
a) Vecteur densité volumique de courant
Vecteur densité volumique de courantVecteur densité volumique de courant
Vecteur densité volumique de courant :
::
:
j n q v
=
Tel que :
I j d S
= ⋅
∫∫
Dimension :
3 2
1
m I
j n q v C s
m m
= = =
en A.m
-2
b
bb
b)
) )
) Loi d’Ohm locale
Loi d’Ohm localeLoi d’Ohm locale
Loi d’Ohm locale :
::
:
En régime permanent :
1
j E E
σρ
= ⋅ = ⋅
(Global
U R I
= ⋅
)
Mais en régime permanent :
2
n q
j n q v E
m
τ
= = ⋅
2 2
n q n e
m m
τ τ
σ ⇒= =
III.3
III.3III.3
III.3 Résistance électrique
Résistance électriqueRésistance électrique
Résistance électrique d’un circuit filiforme
d’un circuit filiforme d’un circuit filiforme
d’un circuit filiforme
Exprimons U et I dans un circuit filiforme :
( )
sec sec tion tion
B B B
BA B A A A A
I j dS E dS E S
U V V dV grad V dl E dl E l
σ σ
= ⋅ = ⋅ ⋅ = ⋅ ⋅
= − = = ⋅ = − ⋅ = ⋅
∫∫ ∫∫
∫ ∫ ∫
Lien de proportionnalité entre Tension / Courant = Résistance électrique :
1
BA
fil fil
U
E l l l
R R
I E S S S
ρ
σ σ
⋅ ⋅
= = = ⋅ = =
⋅ ⋅
E
Vitesse limite = Vitesse que vont atteindre
les électrons en régime permanent
I
dS
dSdS
dS
j
Densité volumique de
courant (en A.m
-2
)
Conductivité
(en S.m
-1
)
Champ électrique
(en V.m
-1
)
Résistivité
(en Ω.m)
D
ensité particulaire en m
-3
Charge
en
C
Vitesse
en
m.s
-1
E
l
ll
l
S
SS
S
A
AA
A
B
BB
B
U
UU
U
BA
BABA
BA
En convention récepteur
:
I
II
I

C
CC
Complément au C
omplément au Complément au C
omplément au CH2
H2H2
H25
55
5 :
: :
: Capteur à
Capteur à Capteur à
Capteur à Effet HALL
Effet HALLEffet HALL
Effet HALL
Comment mesurer un champ magnétique
Comment mesurer un champ magnétiqueComment mesurer un champ magnétique
Comment mesurer un champ magnétique ?
??
?
⇒
Avec
Avec Avec
Avec un
un un
un Capteur à
Capteur à Capteur à
Capteur à Effet Hall
Effet HallEffet Hall
Effet Hall
1.
1.1.
1. Description
DescriptionDescription
Description du capteur
du capteur du capteur
du capteur
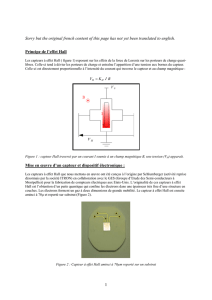
Un capteur à effet Hall est constitué d’une plaque
rectangulaire (d’épaisseur h, et de largeur b) taillée
dans un matériau semi-conducteur dans laquelle on
fait circuler un courant I (capteur actif…).
Lorsqu’il est placé dans un champ magnétique créé
par des sources extérieures (que l’on prendra ici
uniforme
= ⋅
z
B B e
, avec B > 0), une tension apparaît
entre les faces avant et arrière de la plaque,
proportionnelle à l’intensité du champ. Il ne reste qu’à
y brancher un voltmètre et réaliser la converion.
2.
2.2.
2. Conséquences
ConséquencesConséquences
Conséquences :
: :
: C
CC
Champ électrique
hamp électriquehamp électrique
hamp électrique de Hall
de Hall de Hall
de Hall et Tension
et Tension et Tension
et Tension de Hall
de Hallde Hall
de Hall
2.1.
2.1.2.1.
2.1. Hypothèses de travail
Hypothèses de travailHypothèses de travail
Hypothèses de travail
- Le champ magnétique crée par le courant dans la plaque est supposé négligeable devant le champ extérieur,
- La conduction électrique est assurée par des électrons mobiles dont le nombre par unité de volume est noté n.
2.2.
2.2.2.2.
2.2. Vecteur densité de courant
Vecteur densité de courantVecteur densité de courant
Vecteur densité de courant
Le courant I qui circule dans le capteur peut être supposé uniformément réparti sur toute la section de la
plaque. On peut alors le représenter par le vecteur densité volumique de courant uniforme
= ⋅
x
J J e
, toujours
porté par l’axe (Ox) en régime permanent car les électrons ne peuvent ni arriver, ni sortir par l’avant ou l’arrière.
Il est possible d’exprimer ce vecteur
J
en fonction de la vitesse
v
des électrons :
J nq v ne v
= ⋅ = − ⋅
2.
2.2.
2.3
33
3.
..
. En régime transitoire
En régime transitoireEn régime transitoire
En régime transitoire : Accumulation de charges sur les faces avant et arrière
: Accumulation de charges sur les faces avant et arrière: Accumulation de charges sur les faces avant et arrière
: Accumulation de charges sur les faces avant et arrière
L’apparition d’un champ magnétique a
pour effet de dévier le courant électrique
(Force de Lorentz). Ne pouvant pas sortir par
les faces avant et arrière, des charges vont
s’accumuler (négatives à l’avant, positive =
déficit d’électron à l’arrière)
2.
2.2.
2.4
44
4.
..
. En régime permanent
En régime permanentEn régime permanent
En régime permanent : Equilibre de
: Equilibre de: Equilibre de
: Equilibre des
ss
s forces
forces forces
forces
En régime permanent, ce champ de Hall
crée par l’accumulation des charges va
forcément engendrer une force opposée à la
force de Lorentz précédente de manière à
conserver le vecteur densité de courant
parallèle à l’axe (Ox).
2.
2.2.
2.5
55
5.
..
. Mesure du champ mag
Mesure du champ magMesure du champ mag
Mesure du champ magnétique à partir de la mesure de la Ten
nétique à partir de la mesure de la Tennétique à partir de la mesure de la Ten
nétique à partir de la mesure de la Tension de Hall
sion de Hallsion de Hall
sion de Hall
Le champ de Hall
H
E
engendre la tension :
N N
H N M H H H
M M
JB
U V V dV E dy E b U b
ne
= − = = − ⋅ = ⋅ = = ⋅
∫ ∫
(Calcul à partir de la relation potentiel / champ électrique
(
)
=− ⇒=− ⋅
E grad V dV E dl
)
Ainsi :
( )
×
= = ⋅ ⋅ =
× ×
1
H
H H
C
IB b
U I B avec C
b h ne h ne
C H est la constante de Hall ne dépendant que du matériau choisi.
h
b
z
x
B
y
M
N
O
Face 1
(Avant)
Face 2
(Arrière)
Courant I
Courant ICourant I
Courant I
Courant I
Courant ICourant I
Courant I
B
Champ
magnétique extétieur
F
H
E
Champ de Hall
(+ vers le -)
Accumulation de
charges négatives
Courant I
Courant ICourant I
Courant I
B
Accumulation de
charges positives
v
e
ee
e
-
--
-
Vitesse d’un
électron de I
(Force Magnétique)
B
Champ de Hall
Champ de HallChamp de Hall
Champ de Hall :
::
:
⇒= − ∧ = ∧ = ∧ = −
     0 0
1 1 1
0 0
0 0
H
J
E v B J B JB
ne ne ne
B
H y
JB
E e
ne
−
⇒= ⋅
PFD :
+ = + ∧ =
_
0
élec Hall magn H
F F q E qv B
On obtient la valeur du champ magnétique par la mesure de la tension U
H
V
U
H
Courant I
Courant ICourant I
Courant I
B