Logique des prédicats Licence 3 TNM - Semestre 6

Logique des prédicats Licence 3 TNM - Semestre 6
notations: ⊂un sous-ensemble de
⊄pas un sous-ensemble de
∀pour tous les (par exemple: x, pour tout x)∀
⋂intersection
∪union
∆ delta, la différence symétrique
∈appartient à
∉n'appartient pas à
∅ensemble vide
U univers
la complémentarité est indiquée par plusieurs moyens: ~x, ou bien: ^x, ou
encore par une barre supérieure placée au dessus de la lettre.
un sous-ensemble c'est quoi?
F E ssi tous les éléments de F sont aussi des éléments de E.⊂
(x F) (x E)∈ → ∈
x ((x F) (x E))∀ ∈ → ∈
(Fx Ex)→
Il faut savoir que quand on parle d'ensemble, en fait il faudrait toujours parler de sous-
ensemble, car on ne manie jamais l'ensemble.. dans son ensemble.
Définitions préalables
La notion mathématique d’ensemble est une notion primitive, en ce sens qu’elle n’est pas elle-
même définie formellement et qu’elle conserve un statut relativement intuitif. Mais en dépit de cela,
la théorie des ensembles se développe sur une telle notion primitive.
Ensemble et éléments d’un ensemble
Un ensemble est une collection, une famille ou un agrégat d’éléments ou d’objets qui,
eux, sont bien définis.
Théorie des ensembles et algèbre de boole
Les relations
Théorie des ensembles et algèbre de boole (transition entre logique des
propositions du premier semestre et logique des prédicats du second semestre)


Par exemple,
●si A = {1, 2, 3} et B = {3, 4, 5}, alors
A ∪B = {1, 2, 3, 4, 5}
on en conclura que: A = A∪ ∅
et que: A A = A∪
●si A = {1, 2} et B = {3, 4} et C = {5},
alors A B = ∅⋂
B C = B⋂
A C = ∅⋂
●si A = {1, 2} ; B = {3, 4} ; C = {4, 5}
alors A B = ∅⋂
B C = {4}⋂
A C = ∅⋂
La notion de partition et de recouvrement
La notion de recouvrement est définie grâce à celles de réunion, et de sous-ensemble.
En effet, un recouvrement est formé de sous-ensembles d’un ensemble A et dont leur
réunion est égale à A.
Par exemple, si A = {a, b, c} alors {a, b} et {b, c} forment un recouvrement de A, puisque
{a, b} {b, c}∪ = A.
La notion de partition est quant a elle définie grâce aux notions de recouvrement,

d’intersection, de parties, d’ensemble vide et d’ensembles deux a deux disjoints. Une
partition d’un ensemble A est alors définie comme un recouvrement de A formé de
parties non vides de A deux à deux disjointes.
Exemple : Soit A = {1, 2, 3, 4, 5, 6}. Les sous-ensembles {1}, {2, 3, 4} et {5, 6} forment un
recouvrement de A. Ces sous-ensembles sont des parties de A et sont deux à deux
disjoints car leur intersection est vide. Mais chaque sous-ensemble est non vide. Donc
{1}, {2, 3, 4} et {5, 6} forment bel et bien une partition de A.
Produit cartésien, relations et composition des relations
Avant d’entrer dans le vif de notre sujet, il faut introduire une notion préliminaire, celle
de liste. Une liste est une énumération d’objets, symbolisés par des variables
numériques (1, 2, 3, etc.) ou alphabétiques (a, b, c, etc.), et placés entre parenthèses.
Ces objets sont les éléments de la liste. Mais attention ! Une liste n’est pas un ensemble
! Et vice versa ! Les parenthèses sont aux listes ce que les accolades sont aux
ensembles : des moyens de formuler grâce à une syntaxe claire de l’information sur une
structure mathématique quelconque.
Ainsi, une liste peut contenir un seul élément : on l’appelle alors un singlet. Exemple :
(a). Une liste contenant deux éléments, est un doublet ou un couple : (a, b). Si elle
contient trois éléments, il s’agit d’un triplet : (1, 2, c). À quatre éléments, on l’appelle
un quadruplet : (1, 2, c, d). Et ainsi de suite : quintuplet, sextuplet. Si une liste contient
un nombre n d’éléments (c’est-à-dire un nombre indéterminé), elle s’appelle un n-
uplet.
La notion de couple, quant à elle, permet de définir une relation d’ordre, autre notion
capitale dont il faut se souvenir, car l’ordre déterminé entraîne des résultats algébriques
qui autrement ne seraient pas atteints. Ainsi, la notion de couple peut être définie
rigoureusement grâce à la notion de parties d’un ensemble :
Définition de la notion de couple : (a, b) équivalent {{a}, {a, b}}
Ce qui signifie que le couple formé des éléments a et b est équivalent à l’ensemble des
parties de l’ensemble contenant les éléments a et b, c’est-à-dire, en l’occurrence, le
produit cartésien de deux ensembles. Cette particularité du couple permet de définir
l’ordre d’une liste.
En effet, si (a, b) = (c, d), alors a = c et b = d.
Ce qui veut dire ceci : en vertu de l’égalité entre deux couples, les « places » de chacun
de leurs éléments respectifs ne peuvent être changées sans que ne soit affectée
l’égalité entre les couples. Si, par exemple, b ≠ d, alors (a, b) ≠ (c, d) (même chose si a
≠ c). Cette restriction quant à la « place » occupée par un élément dans une liste
quelconque permet d’établir, comme nous le verrons un peu plus loin, les relations entre
ensembles ; et une relation ne souffre d’aucune exception : elle est vérifiée ou ne l’est
pas.
Autre caractéristique : les listes sont finies, c’est-à-dire qu’elles contiennent toujours
un nombre fini d’éléments. Si une liste contient un nombre infini d’éléments, elle sera
alors appelée une suite. Les propriétés des suites seront étudiées plus tard, en temps
opportun.
Produit cartésien
Soit deux ensembles, A et B. Le produit cartésien de A et B est l’ensemble de tous les

couples (x, y) formés quand x A et y B∈ ∈ . Le produit cartésien est noté de la manière
suivante : A x B. Selon la précédente définition et sachant comment noter le produit
cartésien, on voit aisément que l’ensemble formé de ce produit est :
A x B = {(x, y) : x A, y B∈ ∈ }
Cette formule nous dit expressément que tout couple (x, y) est un élément de
l’ensemble produit cartésien A x B et que tout couple est tel à la condition qu’à tout
élément de l’ensemble A, nommé ensemble de départ, correspond un élément de
l’ensemble B, nommé quant à lui ensemble d’arrivée.
Exemple :
Soit A = {a, b, c}, B = {1, 2, 3}. Alors le produit cartésien A x B = {(a, 1), (b, 2), (c, 3)},
correspond à la définition précédemment.
On peut aussi le représenter sous la forme d’un tableau, tel que celui-ci
Soit A = {a, b, c}
B = {1, 2, 3}
A x B = {(a, 1), (b, 2), (c, 3)},
alors A x B :
A/B 1 2 3
a (a, 1) (a, 2) (a, 3)
b (b, 1) (b, 2) (b, 3)
c (c, 1) (c, 2) (c, 3)
Or, le produit cartésien est une opération qui peut également s’exercer d’un ensemble à
lui-même. Ce produit est alors appelé carré cartésien, et est noté : A x A, ou A^2.
Relations entre ensembles
Une relation entre ensembles est définie comme une dépendance de l’une envers
l’autre. Cette dépendance, c’est-à-dire cette relation, est ordonnée.
Une relation d’un ensemble A vers un ensemble B est alors caractérisée comme étant un
sous-ensemble du produit cartésien A×B. (Une telle relation est également appelée «
relation binaire ».)
Ce qui veut dire que l’ensemble de tous les couples formés grâce à la relation R sont
inclus dans A×B, soit : R = {(a, b) : {{a}, {a, b}} ⊂ A x B}
 6
6
 7
7
 8
8
 9
9
 10
10
 11
11
 12
12
 13
13
 14
14
 15
15
 16
16
 17
17
 18
18
 19
19
 20
20
 21
21
 22
22
 23
23
 24
24
 25
25
 26
26
 27
27
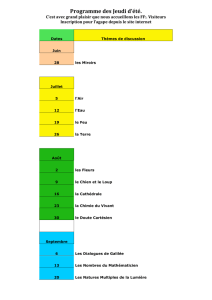
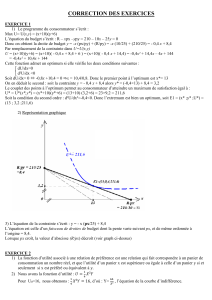
 28
28
 29
29
 30
30
 31
31
 32
32
1
/
32
100%