Fonctions : logarithmes, exponentielles

5. FONCTIONS LOGARITHMES, EXPONENTIELLES,
HYPERBOLIQUES ET HYPERBOLIQUES
RECIPROQUES.
1. Fonction logarithme népérien.
1.1. Définition.
La fonction logarithme népérien, notée ln , est la primitive sur 0,+∞
] [
qui s'annule pour
x=1
de la fonction
xa1
x
.
Soit pour x ∈0, +∞
] [
lnx =dt
t
1
x
∫
.
1.2. Premières propriétés.
•
ln1 =0
• La fonction logarithme est dérivable sur 0,+∞
] [
et (lnx)' =1
x>0
donc la fonction logarithme est continue sur 0,+∞
] [
• la fonction ln est strictement croissante sur 0,+∞
] [
En appliquant la définition de la dérivée en x=1, on a lim
h
→0
ln(1+h)
h=1
Si u est une fonction dérivable sur un intervalle I et ne s'annule pas sur I, on a
∀x∈Iln u(x)
[ ]
'=u' (x)
u(x) et donc ∀x≠0 ln x
[ ]
'=1
x

U.M.N. 5. Logarithmes, exponentielles, hyperboliques et réciproques. Cours.
©dpic - inpl - mars 1999
2
1.3. Autres propriétés.
• ∀x>0∀x' >0ln(xx' )=lnx +lnx'
• ∀x>0ln(1
x)= −lnx
• ∀x>0∀x' >0 ln( x
x' )=lnx−lnx'
•
∀x>0∀r∈Qln(x r)=rlnx
La fonction logarithme est une bijection de 0,+∞
] [
sur −∞,+∞
] [
, on a donc
lnx1=lnx2
x1>0et x2>0
⇔
x1=x2
x1>0 et x2>0
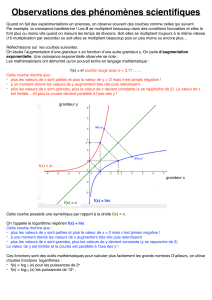
1.4. Tableau de variations
lim
x
→+∞
lnx
x=0
Quand x tend vers
+∞
, la courbe présente une branche parabolique dans la direction Ox.
1.5. Définition du nombre e
La fonction logarithme étant une bijection de 0,+∞
] [
sur −∞,+∞
] [
, il existe un nombre
unique appelé e tel que
lne =1
.
La valeur décimale approchée de e à
10−5
près par défaut est 2,71828.
x
+
f ’(x)
ln(x)
−∞
+∞
+∞
10
0

U.M.N. 5. Logarithmes, exponentielles, hyperboliques et réciproques. Cours.
©dpic - inpl - mars 1999
3
1.6. Courbe représentative.
2. Fonction exponentielle
La fonction logarithme étant une bijection de 0,+∞
] [
sur −∞,+∞
] [
, elle admet une fonction
réciproque appelée exponentielle et notée
exp (ou x aex)
y=ex
x∈−∞,+∞
] [
⇔
x=lny
y∈0,+∞
] [
2.1. Propriétés
• ∀x∈0,+ ∞
] [
elnx =x
• ∀x∈−∞,+∞
] [
ln(ex)=x
• ∀x∈ −∞,+∞
] [
ex>0
•
e0=1
La fonction exponentielle est continue et dérivable sur R et on a :
∀x∈−∞,+∞
] [
(ex)' =ex
Si u est une fonction dérivable sur un intervalle I, on a
∀x∈I eu(x)
[ ]
'=u' (x)eu(x)

U.M.N. 5. Logarithmes, exponentielles, hyperboliques et réciproques. Cours.
©dpic - inpl - mars 1999
4
Formules d'addition.
∀x∈R∀x' ∈Rex+x' =exex'
et
∀x∈Re−x=1
ex
lim
x
→+∞ ex= +∞ lim x→−∞ex=0
Donc quand x tend vers
+∞
, la courbe présente une branche parabolique dans la direction Oy;
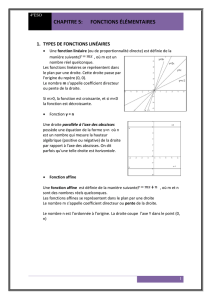
2.2. Courbe représentative :
En repère orthonormé, la courbe représentative de la fonction exponentielle est symétrique de
celle de la fonction logarithme par rapport à la première bissectrice
3. Fonction logarithme et exponentielle de base A.
Théorème : Logarithme de base a
Soit a∈0,+ ∞
] [
−1 { }
, on appelle fonction logarithme de base a et on note loga la fonction
définie par
∀x>0 logax=lnx
lna
En particulier le logarithme népérien est le logarithme en base e.

U.M.N. 5. Logarithmes, exponentielles, hyperboliques et réciproques. Cours.
©dpic - inpl - mars 1999
5
Théorème :
Le logarithme de base 10 est appelé logarithme décimal et noté log
Propriétés
• La fonction logarithme de base a est continue, strictement monotone sur 0,+∞
] [
• loga1=ln1
lna =0logaa=lna lna =1
• (logax)' =1
xlna ∀x∈0, +∞
] [
• La fonction loga est dérivable sur 0,+∞
] [
et logax ( ) =lnx
lna
 '=1
xlna
• si a >1 alors logaest strictement croissante
• si a <1 alors logaest strictement décroissante
• ∀x>0∀x' >0 loga(xx') =logax+logax'
• ∀x>0∀x' >0 loga(x
x' )=logax−logax'
•
∀x>0∀r∈Qloga(xr)=rlogax
Changement de base :
∀(a, b) ∈0, +∞
] [
−1 { }
( )
2,∀c∈0, +∞
] [
logac=logab.logbc
3.1. Exponentielle de base a.
a∈0,+ ∞
] [
−1 { }
, la fonction loga est continue, strictement monotone sur 0,+∞
] [
. Elle
admet donc une fonction réciproque appelée exponentielle de base a et notée
expaou x aax
y=ax
x∈−∞,+∞
] [
⇔
x=logay
y∈0,+∞
] [
ou encore x=logay=lny
lna et lny =xlna
∀x∈Ry=ax=exlna