Page 1 of 3 0

Page 1 of 3
T-2
Q
Le Principe d’Extremum (Total: 10 Points)
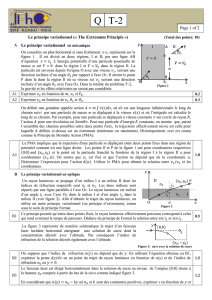
A. Le Principe d’Extremum en Mécanique
Figure 1
Soit un plan horizontal x-y sans frottements, illustré par la Fig. 1. Il est divisé en deux parties, I et II, par la droite
AB satisfaisant l'équation 𝑥 = 𝑥1. L'énergie potentielle d'une particule ponctuelle de masse m dans la partie I est
𝑉=0! tandis que 𝑉=𝑉
! dans la partie II. La particule est envoyée depuis l'origine O à une vitesse 𝑣1, le long
d'une droite formant un angle 𝜃! avec l'axe x. Elle arrive au point P dans la partie II en y ayant voyagé à une vitesse
𝑣! le long d'une droite qui fait un angle 𝜃!!avec l'axe x. Il faut ignorer la gravité et les effets relativistes dans tout ce
problème.
A1
Obtenir une expression pour 𝑣! en fonction de 𝑚, 𝑣! et 𝑉
!!!
0.2
A2
Exprimer!!𝑣!!en fonction de 𝑣!, 𝜃!!et 𝜃!.
0.3
Définissons une quantité appelée action 𝐴=𝑚𝑣(𝑠)𝑑𝑠, où ds est une longueur infinitésimale sur la trajectoire
d'une particule de masse 𝑚 qui se déplace à la vitesse 𝑣(𝑠). L'intégrale est prise le long de la trajectoire. Par
exemple, pour une particule se déplaçant à vitesse constante sur une trajectoire circulaire de rayon 𝑅, 𝐴 vaudra
2𝜋𝑚𝑅𝑣 pour un tour complet. Pour une particule d’énergie constante 𝐸, il peut être démontré que, parmi toutes les
trajectoires possibles entre deux points fixes, la vraie trajectoire est celle sur laquelle 𝐴, définie ci-dessus, est un
extremum (maximum ou minimum). Historiquement, ce principe est connu sous le nom de Principe de Moindre
Action (PMA).
A3
Le PMA implique que la trajectoire d'une particule se déplaçant entre deux points fixes dans une région
de potentiel constant est une ligne droite. Soient les deux points fixes 𝑂 et 𝑃 de la Fig. 1 de coordonnées
(0,0)!et (𝑥!,𝑦!) respectivement et le point frontière 𝑥!,𝛼 où la particule passe de la partie I à la partie
II. Notez que 𝑥! est fixé et que l’action dépend uniquement de la variable 𝛼. Donnez l'expression de
l'action 𝐴(𝛼). Utiliser le PMA pour obtenir la relation entre 𝑣!/𝑣! et les coordonnées définies ci-dessus.
1.0
B. Le Principe d’Extremum en Optique
Un rayon lumineux passe du milieu I au milieu II d’indices de réfraction 𝑛! et 𝑛 respectivement. Les deux milieux
sont séparés par une droite parallèle à l'axe x. Le rayon de lumière fait un angle 𝑖! avec l'axe y dans le milieu I et
un angle 𝑖 dans le milieu II (voir Fig. 2). Pour déterminer la trajectoire du rayon, nous nous servons d'un autre
principe d’extremum appelé le principe du moindre temps de Fermat.

Page 2 of 3
T-2
Q
Figure 2
B1
Le principe de Fermat affirme que la trajectoire d’un rayon lumineux entre 2 points fixes est telle que le
temps nécessaire à son parcours soit un extremum. Déduisez la relation entre 𝑠𝑖𝑛!𝑖!!et 𝑠𝑖𝑛 𝑖! sur base
du principe de Fermat.
0.5
La Fig. 3 illustre la trajectoire d'un faisceau laser dirigé horizontalement à
travers une solution dans laquelle la concentration en sucre diminue avec la
hauteur. En conséquence l'indice de réfraction de la solution diminue
également quand la hauteur augmente.
Figure 3 : bac contenant une solution de sucre
B2
Supposez que l'indice de réfraction 𝑛(𝑦) ne dépend que de 𝑦. Utilisez l'équation obtenue en B1 pour
obtenir l'expression de la pente 𝑑𝑦/𝑑𝑥 de la trajectoire du faisceau en fonction de 𝑛! (indice de
réfraction à 𝑦=0) et 𝑛(𝑦).
1.5
B3
Le faisceau laser est dirigé horizontalement à travers la solution sucrée depuis l'origine (0,0) à une
hauteur 𝑦! du fond de la cuve, comme illustré sur la Fig 3. Posons 𝑛𝑦=𝑛!−𝑘𝑦 où 𝑛! et 𝑘 sont des
constantes positives. Déterminez la trajectoire du faisceau sous la forme d’une expression de 𝑥 en
fonction de 𝑦 et des grandeurs associées. Vous pouvez utiliser la relation : 𝑠𝑒𝑐𝜃𝑑𝜃 =ln!(sec 𝜃+
tan 𝜃)+constante, où secθ=1/cosθ ou alors !"
!!!!
=ln 𝑥+𝑥!−1+𝑐𝑜𝑛𝑠𝑡𝑎𝑛𝑡𝑒.
1.2
B4
Donnez la valeur de 𝑥!, le point d’impact du faisceau sur le fond de la cuve. Prenez 𝑦!=10.0!cm,
𝑛!=1.50, et 𝑘=0.05!cm!! (1 cm = 10-2 m).
0.8
C. Le Principe d’Extremum et la nature ondulatoire de la matière
Nous explorons ici la connexion entre le PMA et la nature ondulatoire d’une particule en mouvement. Pour cela,
nous supposons qu'une particule se déplaçant de 𝑂 à 𝑃 peut prendre toutes les trajectoires possibles. Nous
chercherons une trajectoire définie par l'interférence constructive des ondes de Broglie.
C1
Dans le cas d’une particule se déplaçant le long de sa trajectoire sur une distance infinitésimale Δ𝑠,
reliez la variation de phase Δ𝜑! de son onde de Broglie à la variation d’action Δ𝐴!.
0.6
(𝑥
!
,−𝑦
!
)
(0,0)
𝑥
𝑦

Page 3 of 3
T-2
Q
C2
Revenons au problème de la section A dans lequel la particule se déplace de 𝑂 à 𝑃 (voir Fig. 4). Plaçons
une séparation opaque sur la limite 𝐴𝐵 entre les parties I et II.
Elle présente une petite ouverture 𝐶𝐷 de largeur 𝑑 telle que
𝑑≪(𝑥!−!𝑥!) et 𝑑≪𝑥!. Considérez deux trajectoires
extrêmes 𝑂𝐶𝑃 et 𝑂𝐷𝑃 telle que 𝑂𝐷𝑃 se trouve sur la
trajectoire classique décrite dans la section A. Déterminez la
différence de phase ∆𝜑!" entre les deux trajectoires en
simplifiant au premier ordre.
Figure 4
1.2
D. Interférence d'ondes associées à la matière
Soit un canon à électrons situé en 𝑂 qui dirige un faisceau
collimaté d'électrons dans une fente étroite 𝐹 de la séparation
opaque 𝐴!𝐵! située à 𝑥!=!𝑥!. 𝑂𝐹𝑃 est une ligne droite et 𝑃 un
point de l'écran situé à 𝑥=!𝑥! (voir Fig. 5). La vitesse dans la
partie I est 𝑣!=2.0000×10! m s!! et 𝜃!=10.0000°. Le
potentiel 𝑈!!en II est tel que la vitesse 𝑣!=1.9900×10!!m s!!.
La distance 𝑥!−𝑥! est 250.00!mm (1mm!=!10!!m). Ignorez
l'interaction électron-électron.
Figure 5
D1
Si les électrons issus de 𝑂 ont été accélérés depuis l’état de repos, calculez le potentiel électrique 𝑈!.
0.3
D2
Une autre fente identique 𝐺 est pratiquée dans la séparation 𝐴!𝐵! à une distance de 215.00!nm
(1nm =10!!m) au-dessous de la fente 𝐹 (voir Fig. 5). Si la différence de phase entre les ondes de
Broglie arrivant en P à travers les fentes F et G vaut 2𝜋𝛽 , calculez 𝛽.
0.8
D3
Quelle est la plus petite distance ∆𝑦 mesurée depuis P à laquelle on ne détecte pas d’électron sur
l’écran? [Remarque : l’approximation sin 𝜃+Δ𝜃≈sin 𝜃+Δ𝜃cos 𝜃 peut vous être utile].
1.2
D4
Le faisceau a une section transversale carrée de 500nm×500nm et l’installation a une longueur de 2 m.
Quelle devrait être la densité de flux minimum Imin (nombre d’électrons par unité de surface normale et
par unité de temps), si, à un moment donné, il y a en moyenne au moins un électron dans cet
appareillage ?
0.4
*****
A
B
I
II
P
C
D
CD=d
(𝑥
!
,𝑦
!
)
𝑉
=𝑉
!
𝑉=0
O
𝑦
𝑥
𝑥
!
𝑦
O
𝑥
𝑥!
𝑥!
I
II
A!
B!
10°
F
G
215.00&nm&
P
250&mm&