notes_cours_geometrie_transformations

Notes – Géométrie
2016
1
Copyright – Tous droits réservés https://mamanfuturemaitresse.wordpress.com
© Mélodie VERGES
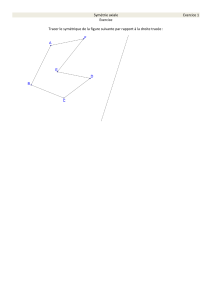
Transformations du plan
Symétrie axiale (= symétrie orthogonale par rapport à une droite)
F et F’ étant deux figures dessinées sur une feuille, F’ est le symétrique de F par rapport à une droit (d) si, lorsqu’on
plie la feuille en suivant (d), F et F’ se superposent parfaitement.
Le symétrique de F par rapport à la droite (d) est l’ensemble F’ de toutes les images des points de F par cette
symétrie. (figure 1)
Une figure F admet un axe de symétrie (d) si le symétrique de tout point de F par rapport à (d) appartient à F.
Le symétrique d’un point E par rapport à une droite (d) est :
- Le point F tel que (d) soit la médiatrice de [EF] si E n’est pas sur (d) (figure 2)
- Le point E lui-même si E est sur (d) (E est alors un point invariant) (figure 3)
On dit alors que F est l’image de F par la symétrie d’axe (d) ; que E et F sont symétriques par rapport à (d)
Figure 1 Figure 2 Figure 3
Figure 4 Figure 5 Figure 6
Propriétés :
- Conservation de l’alignement : l’image d’une droite par une symétrie axiale est une droite. (figure 2)
- Conservation des longueurs : l’image d’un segment par une symétrie axiale est un segment de même
longueur. (figure 4)
- Conservation du milieu : l’image du milieu d’un segment par une symétrie axiale est le milieu de l’image de ce
segment. (figure 4)
- Conservation des angles : l’image d’un angle par une symétrie axiale est un angle de même mesure. Ainsi la
symétrie axiale conserve l’orthogonalité. (figure 5)
- Conservation du parallélisme : l’image de deux droites parallèles par une symétrie axiale est formée de deux
droites parallèles. (figure 6)

Notes – Géométrie
2016
2
Copyright – Tous droits réservés https://mamanfuturemaitresse.wordpress.com
© Mélodie VERGES
Symétrie centrale (= symétrie par rapport à un point)
Une figure F’ est le symétrique d’une figure F par rapport à un point C si on obtient F’ en faisant tourner F de 180°
autour de C. (figure 1). Le symétrique d’une figure F par rapport à un point est l’ensemble F’ de toutes les images des
points de f par cette symétrie. (figure 1)
Une figure F admet un centre de symétrie C si le symétrique de tout point de F appartient à F.
Le symétrique d’un point M par rapport à un point C est :
- Le point M’ tel que C soit le milieu de [MM’] si M est distinct de C. (figure 2)
- Le point M lui-même si M et C sont confondus
Figure 1 Figure 2
Figure 3 Figure 4 Figure 5 Figure 6
Propriétés :
- Conservation de l’alignement : l’image d’une droite par une symétrie axiale est une droite. (figure 3)
- Conservation des longueurs : l’image d’un segment par une symétrie axiale est un segment de même
longueur. (figure 4)
- Conservation du milieu : l’image du milieu d’un segment par une symétrie axiale est le milieu de l’image de
ce segment. (figure 4)
- Conservation des angles : l’image d’un angle par une symétrie axiale est un angle de même mesure. Ainsi la
symétrie axiale conserve l’orthogonalité. (figure 5)
- Conservation du parallélisme : l’image de deux droites parallèles par une symétrie axiale est formée de deux
droites parallèles. (figure 6)
- Quelle que soit la droite, la symétrie centrale transforme cette droite en une droite parallèle. (figure 3)

Notes – Géométrie
2016
3
Copyright – Tous droits réservés https://mamanfuturemaitresse.wordpress.com
© Mélodie VERGES
Agrandissement/réduction d’une figure
Un polygone F’ est un agrandissement/réduction d’un polygone F si les dimensions de ses
côtés ont été multipliées par un même coefficient réel positif et que les angles sont
conservés.
Si le coefficient est >1, on obtient un agrandissement.
Si le coefficient est <1, on obtient une réduction.
Translation
Une figure F’ est l’image d’une figure F par une translation s’il est possible, en faisant glisser F sans la faire tourner,
de la faire coïncider avec F’. (figure 1)
Etant donné deux points A et B, on appelle translation l’application du plan dans lui-même qui à tout point de M
associe le point M’ tel que ABMM’ soit un parallélogramme. (figure 2)
Figure 1 Figure 2 Figure 3 Figure 4
Propriétés :
- Conservation de l’alignement
- Conservation des longueurs
- Conservation du milieu
- Conservation des angles (et donc de l’orthogonalité)
- Conservation du parallélisme
- Linéarité de la proportionnalité : si dans la figure un côté est la somme de deux autres côtés, alors il en est
de même de leurs agrandissements/réductions respectifs ; si dans la figure un côté est k fois plus long qu’un
autre côté, alors il en est de même de leurs agrandissements/réductions respectifs.
Propriétés :
- Conservation de l’alignement (figure 1)
- Conservation des longueurs (figure 1)
- Conservation du milieu
- Conservation des angles (et donc de l’orthogonalité)
- Conservation du parallélisme (figures 1, 2, 3)
- L’image d’une droite est une droite parallèle (figure 3)
- L’image d’un cercle est un cercle de même rayon dont le centre est l’image du centre. (figure 4)

Notes – Géométrie
2016
4
Copyright – Tous droits réservés https://mamanfuturemaitresse.wordpress.com
© Mélodie VERGES
Rotation
Définir une rotation demande d’abord de définir son sens de rotation. On distingue de sens direct : dans le sens
inverse des aiguilles d’une montre, sa mesure est positive ; et de sens indirect dont la mesure est négative.
Une figure F’ est l’image d’une figure F par une rotation de centre C et d’angle 𝜃 de sens direct/indirect si, lorsqu’on
fait tourner la figure F d’un angle 𝜃 de sens direct/indirect autour de C, alors elle se superpose avec F’. (figure 1)
Etant donné un angle 𝜃 de sens direct/indirect et un point C, l’image du point M par la rotation
de centre C et d’angle 𝜃 est :
- Le point M’ tel que CM’=CM et l’angle (𝐶𝑀’𝐶𝑀
̂) = 𝜃 de sens direct/indirect si M est
différent de C,
- Le point M lui-même si M est en C.
La rotation de centre C et d’angle 𝜃 est notée R(C, 𝜃). Si M’ est l’image de M par R(C, 𝜃), on
écrit : M’= R(C, 𝜃) (M)
Homothétie de rapport positif
Soit un nombre k ≠ 0 et un point C, l’image d’un point M par l’homothétie de centre C et de
rapport k est le point M’ tel que M’ est sur la demi-droite [CM) et CM’ = k ∞ CM
L’homothétie de centre C et de rapport k est notée H(C,k).
Une homothétie de rapport k >1 agrandit la figure.
Une homothétie de rapport k <1 réduit la figure.
Propriétés :
- Conservation de l’alignement
- Conservation des longueurs
- Conservation du milieu
- Conservation des angles (et donc de l’orthogonalité)
- Conservation du parallélisme
- L’image d’une droite par une rotation n’est généralement pas une droite parallèle.
- L’image d’un cercle est un cercle de même rayon dont le centre est l’image du centre.
Propriétés :
- Conservation de l’alignement
- Conservation de l’égalité des longueurs : des segments de même longueur auront des images de même
longueur
- Conservation du milieu
- Conservation des angles (et donc de l’orthogonalité)
- Conservation du parallélisme
- L’image d’une droite par une homothétie est une droite parallèle.