Correction du contrôle sur la symétrie centrale Exercice 1 : 1) Ces

Correction du contrôle sur la symétrie centrale
Exercice 1 :
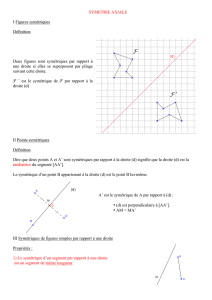
1) Ces deux angles sont symétriques car ils ont la
même mesure et leurs côtés sont parallèles. Le centre
de la symétrie est le point O, qui est le milieu du
segment joignant les sommets des deux angles.
2) Ces deux segments ne sont pas symétriques par une
symétrie centrale, car ils ne sont pas parallèles (même
si ils sont de même longueur).
3) Construire le symétrique de la droite (d) par
rapport à F.
Vous laisserez les traits de construction.
(voir cours et exercices, déjà faits plusieurs fois)
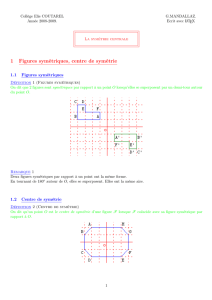
Exercice 2 : 1) M est le milieu de [OH], donc O et H sont symétriques
par rapport à M, et les deux cercles ont le même rayon,
donc ils sont symétriques par rapport à M.
2) Les points S et T appartiennent au cercle C1 , donc
leurs symétriques appartiennent au cercle C2 .
Comme un point, son symétrique et le centre de
symétrie sont alignés :
U est le point d'intersection de C2 et de (SM) ;
V est le point d'intersection de C2 et de (TM).
Exercice 3 : Reconnaître et différencier la
symétrie axiale et la symétrie centrale :
ABCD, AEDJ, AEBK et EBLC sont des carrés de
centres respectifs E, I, F et G.
Les points F, G, H et I sont les milieux des côtés du
carré ABCD.
Compléter le tableau en indiquant la symétrie
axiale, en précisant l'axe, ou, la symétrie centrale,
en précisant le centre, qui permet de passer de la
figure de départ à la figure image.
Figure de départ Figure image Type de symétrie avec précision
AFE EHC Symétrie de centre E
DIE ECG Symétrie d'axe (EH)
DEH EGB Symétrie d'axe (EC)
AEJ CLE Symétrie de centre E
DIJ BLG Symétrie de centre E

Exercice 4 : Utiliser les propriétés de la symétrie centrale pour prouver
1) 4 + 5 = 9 >7 donc d'après l'inégalité triangulaire, le triangle BUT existe, car la somme du petit côté et du
moyen côté est supérieure au grand côté.
2) Construire le triangle BUT.
3) Construire le point H milieu du segment [BU].
4) Compléter :
On sait que H est le milieu du segment [BU], donc B et U sont symétriques par rapport à H.
5) Construire R le symétrique de T par rapport à H.
6) a) Compléter :
Le symétrique de B par rapport à H est U
Le symétrique de T par rapport à H est R
Donc le symétrique du segment [BT] par rapport à H est [UR].
Donc BT = UR, car (propriété) le symétrique d'un segment est un segment de même longueur.
Donc (BT) // (UR) , car (propriété) le symétrique d'un segment est un segment qui lui est parallèle.
8) BT = UR et (BT) // (UR), or , si un quadrilatère non croisé à deux côtés opposés parallèles et de même
mesure, alors c'est un parallélogramme. Donc le quadrilatère BRUT est un parallélogramme.
------------------------------------------------------------------------------------------------------------------------------------