Fiche Élève - Gradus ad Mathematicam

Suite de Syracuse avec
Xcas, scilab, Casio ou T.I.
Fiche Élève
1ère
Auteur : PL
On définit une suite de la manière suivante :
– premier terme : choisir un entier naturel non nul n.
– deuxième terme : si nest pair, ce sera n
2·Sinon, ce sera 3n+ 1.
– termes suivants : recommencer la procédure pour obtenir les termes suivants.
À l’heure actuelle, on ignore si, pour tout entier naturel non nul n, la suite des valeurs successives as-
sociée à ncomporte la valeur 1. Dans ce cas, la suite continuerait indéfiniment en prenant les valeurs
4,2,1,4,2,1, . . . Ci-dessous, nous arrêtons la liste dès que 1 est atteint, ce qui se produit toujours d’après
une conjecture dite conjecture de Syracuse. La suite ainsi arrêtée au premier 1 rencontré s’appelle suite de
Syracuse de n.
Exemple : La suite de Syracuse de 13 est 40,20,10,5,16,8,4,2,1.
Un vocabulaire aéronautique est utilisé pour décrire la suite de Syracuse d’un entier naturel non nul n.
Ainsi, on dit que cette suite est le vol de n, le nombre de ses termes est la durée du vol, le terme le plus
grand du vol est son altitude maximale (*).
Exemple :13 a un vol de durée 9, son altitude maximale est 40.
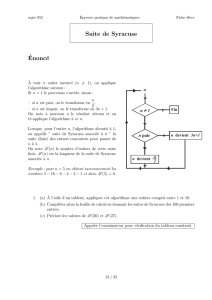
On considère donc l’algorithme suivant :
Algorithme : Suite de Syracuse
Entrée : n, un entier naturel non nul
Sorties : suite de Syracuse de n, durée du vol, altitude maximum
Lire : n
Début du traitement des données :
tant que n6= 1 faire
si nest un nombre pair alors
nprend la valeur n/2
sinon
nprend la valeur 3n+ 1
Afficher : les valeurs successives de n, le nombre de ces valeurs, le maximum de ces valeurs
Fin du traitement des données
Question : écrire un programme associé à l’algorithme ci-dessus dans un langage de programmation.
(*) voir « Pour la science » no247