PHY 11a_Electricité_1ère Session_2013-2014

1
Examen d’électricité (décembre 2013)
Calculette, dictionnaire de langue et feuille A4 manuscrite autorisés.
Téléphone portable interdit.
Rendre les copies Radioactivité et Electricité sur des feuilles séparées.
Les 4 exercices d’électricité sont indépendants et seront notés sur 23 points. Il n’est donc
pas nécessaire d’avoir tout fait pour avoir 20/20 !
Données générales :
Nombre d’Avogadro : N
A
= 6,02 × 10
23
mol
-1
Constante diélectrique du vide : ε
0
= 8,85 × 10
-12
SI
Constante de Boltzmann : k
B
= 1,38 × 10
-23
J/K
Equivalence °C et K : 25 °C = 298 K
Charge élémentaire : e = 1,60 × 10
-19
C
Exercice 1 : champ et potentiel électriques créés par trois ions (sur 6 points).
Soient deux ions Na
+
et un ion O
2-
disposés comme indiqué sur la figure ci-dessous.
1/ En supposant que les nuages électroniques de chacun des ions sont à symétrie sphérique,
déduire un modèle de charges ponctuelles équivalent aux trois ions.
2/ Donner l’expression du potentiel électrique créé au point M par les trois ions en fonction de
a et b. Faire l’application numérique pour a = 2Å et b = 4Å.
3/ Construire le champ électrique créé par les trois ions au point M. Vous reproduirez le
dessin sur votre copie. En déduire la direction et le sens du champ électrique.
4/ Donner l’expression de l’intensité du champ électrique au point M en fonction de a et b.
5/ En déduire la force exercée sur un ion Cl
-
placé en M (direction, sens et intensité). Faire
l’application numérique pour a = 2Å et b = 4Å.
Ion Na
+
a
a
M
Ion Na
+
b
Ion O
2
-

2
Exercice 2 : limite de potabilité de l’eau (sur 5 points)
La potabilité d’une eau dépend de nombreux critères mais peut s’évaluer en mesurant sa
conductivité électrique. On considère qu’une eau devient non potable quand sa conductivité
dépasse 1mS/cm à 25°C.
On donne le tableau suivant pour les mobilités de quelques ions à 25°C dans l’eau, dans la
limite des très faibles concentrations :
Cations µ (10
-5
cm
2
V
-1
s
-1
) Anions µ (10
-5
cm
2
V
-1
s
-1
)
H
3
O
+
Li
+
Na
+
K
+
Ca
2+
362,3
40,1
51,9
76,2
61,6
OH
-
Cl
-
Br
-
CH
3
COO
-
SO
42-
-206,4
-79,1
-80,9
-42,4
-82,9
1/ On suppose que la source de pollution principale de l’eau provient d’ions Ca
2+
et SO
42-
en
concentration égale. En déduire la concentration molaire (en mol/ℓ) de ces ions à la limite de
potabilité, c'est-à-dire quand la conductivité est égale à 1mS/cm. On rappelle que 1S = 1Ω
-1
.
2/ On souhaite contrôler la potabilité de l’eau en mesurant en permanence la résistance d’une
cellule de conductimétrie. On utilise une cellule de conductimétrie de constante de cellule k =
0,100cm. Quelle valeur de résistance R
seuil
correspond à la limite de potabilité de l’eau (on
rappelle qu’on a la relation G = kσ, où G est la conductance) ? Si on veut déclencher une
alarme quand l’eau devient non potable, doit-on déclencher l’alarme quand R > R
seuil
ou
quand R < R
seuil
?
3/ La mesure de résistance a une précision de 5% et la constante de cellule, une précision de
2%. Déterminer les incertitudes relatives et absolues sur R
seuil
. Si on déclenche l’alarme en se
basant sur une mesure de R
seuil
, de combien de % la concentration en ions pourra s’écarter de
la valeur correspondant à la limite de potabilité ?

3
Exercice 3 : énergie potentielle électrostatique d’interaction entre un dipôle permanent
et une molécule (sur 5 points)
1/ On donne l’échelle d’électronégativité simplifiée suivante :
Quels sont les signes des charges portées par les atomes H et Cl dans la molécule HCl ?
2/ On donne le moment dipolaire de la molécule HCl : mCp
HCl
.1061,3
30−
×= et la distance
entre H et Cl : d
HCl
= 1,26Å. Calculer les charges δ
Η
et δ
Cl
portées par les atomes H et Cl.
On place la molécule HCl à proximité d’une molécule linéaire qui peut se modéliser par trois
charges e, -2e et e ponctuelles et placées respectivement en O
1
, O
2
et O
3
(voir la figure ci-
dessous).
On donne O
1
O
2
= O
2
O
3
= O
2
H = 2Å.
3/ Calculer en eV l’énergie potentielle électrostatique d’interaction entre les deux molécules.
S’agit-il d’une liaison électrostatique ? Si oui, donner l’énergie de liaison et commenter la
« force » de la liaison.
e -2e e
H
O
1
O
2
O
3
Cl
H
C
N
Cl
O
+ électronégatif

4
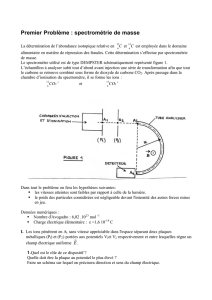
Exercice 4 : spectrométrie de masse à temps de vol et spectrométrie de mobilité ionique.
Les parties 1 et 2 sont indépendantes (sur 7 points).
1/ Spectromètre de masse à temps de vol
Dans un spectromètre de masse dit à « temps de vol », des molécules ionisées sont introduites
sans vitesse initiale en O
1
, à l’extrémité du tube d’accélération. Elles sont alors accélérées
dans le tube d’accélération par un champ électrique uniforme créé entre deux électrodes
portées aux potentiels V
1
et V
2
(les électrodes sont des disques métalliques percés par des
petits trous au centre qui ne modifient pas significativement les lignes de champ électrique).
Elles traversent ensuite une zone de champ nul, le tube de vol, à la sortie duquel elles sont
finalement détectées. Le tube d’accélération et le tube de vol sont maintenus sous vide.
Schéma de principe (vue en coupe) d’un spectromètre de masse à temps de vol. Les ions se déplacent
de la source vers le détecteur le long de l’axe (Ox).
1.1/ En supposant que le champ électrique
E
r
est uniforme partout dans le tube d’accélération,
écrire la relation entre ∆V = |V
1
- V
2
|, E
r
et L
a
. Quel doit être le signe de V
1
- V
2
pour
permettre la détection d’ions de charge Q > 0 ?
1.2/ Montrer que la vitesse v d’un ion en sortie du tube d’accélération (en O
2
) a pour
intensité :
mVQ
v∆ =2
r
.
1.3/ En déduire l’expression du temps de vol t
v
(temps écoulé depuis l’entrée de l’ion dans le
tube de vol en O
2
et son arrivée dans le détecteur en O
3
) en fonction de Q, ∆V, m et L
v
.
1.4/ Application numérique. Soit ∆V = 15kV et L
v
= 1,5m. On injecte en O
1
un ion de
bradykinine de charge Q = 2e. On mesure un temps de vol t
v
de 20,5µs. En déduire la masse
de l’ion de bradykinine.
Source
d’ions
L
a
Détecteur Tube de vol
Tube d’
accélération
x
L
v
O
1
O
2
O
3
V
1
V
2
V
1
V
2

5
2/ Spectromètre de mobilité ionique
Dans le cas de la spectrométrie de mobilité ionique, les molécules ionisées sont également
accélérées par un champ électrique mais en présence d’un gaz neutre (par exemple de
l’hélium sous basse pression).
Schéma de principe (vue en coupe) d’un spectromètre à mobilité ionique. Les ions se déplacent de la
source vers le détecteur dans le tube de mobilité sous une pression d’hélium gazeux.
2.1/ En supposant que le champ électrique est uniforme partout dans le tube, écrire la relation
entre ∆V = |V
1
- V
2
|, E
r
et L. Quel est le signe de (V
1
– V
2
) dans cette expérience pour
permettre la détection d’ions de charge Q > 0 ?
2.2/ Soit un tube de mobilité tel que ∆V = 1000V et L = 1m. On injecte en O
1
un ion de
bradykinine de charge Q = 2e sans vitesse et on le détecte en O
2
à la sortie du tube 32ms plus
tard. En déduire la mobilité ionique des ions de bradykinine.
2.3/ Le coefficient de diffusion d’un ion de bradykinine dans l’Hélium gazeux (dans les
mêmes conditions de pression et de température que dans le tube de mobilité) est
D = 8,0×10
-4
m
2
/s. Quelle est la distance typique parcourue par diffusion par l’ion pendant
32ms ? Pourquoi si on renouvelle l’expérience de la question 2.2, ne trouve-t-on pas toujours
le même temps de migration ?
Source
d’ions Détecteur
Tube de mobilité
x
L
He gazeux
O
1
O
2
V
1
V
2
V
1
V
2