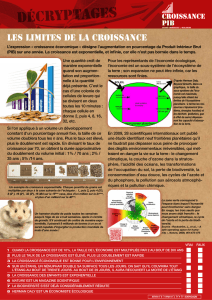
exponentielles

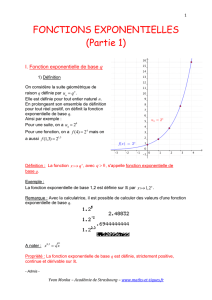
La fonction exponentielle
Le nombre e
On peut démontrer que la suite des nombres
2,9
4,64 27,625 256,7776 3125, . . .
(le terme général est (1 + 1/n)n) admet une limite. Cette limite est un
nombre irrationnel, noté e, qui joue un rôle très important en mathéma-
tiques :
e= lim
n→+∞1 + 1
nn
= 2,71828... (1)
Il possède entre autres la propriété suivante :
quelque soit le nombre x, ex= lim
n→+∞1 + x
nn
.(2)
C’est ainsi qu’est définie la fonction exponentielle. C’est une fonction trans-
cendante dont le calcul des valeurs requiert un passage à la limite (ou l’uti-
lisation d’une calculatrice). D’après sa définition, il est clair que la fonction
exponentielle est croissante. On peut démontrer qu’elle possède la propriété
-1
1
2
3
4
x
10
20
30
40
50
y
y= ãx
fondamentale suivante :
quels que soient les nombres x1et x2, ex1+x2=ex1ex2(3)
1

(la fonction exponentielle transforme les sommes en produits). On en déduit
en particulier que 1
ex=e−x.(4)
Une autre conséquence de la propriété fondamentale est que la fonction
exponentielle croît plus vite que toute puissance de son argument, si grande
soit-elle, lorsque cet argument tend vers +∞.
pour tout exposant nfixé ,lim
x→+∞
ex
xn= +∞.
Lorsque x→ −∞ au contraire, en vertu de la propriété (4), l’exponentielle
5
10
15
20
25
x
5.0´106
1.0´107
1.5´107
2.0´107
2.5´107
y
y= ãx
y=x5
tend vers 0 (très rapidement mais sans jamais l’atteindre car elle ne s’annule
jamais).
2

L’exponentielle est aussi définie pour des valeurs complexes de son argu-
-1
1
2
3
4
x
0.5
1.0
1.5
2.0
2.5
y
y= ã-x
ment (elle prend alors elle même des valeurs complexes). Pour un nombre
imaginaire pur, iy, elle est donnée par la formule d’Euler :
eiy = cos y+isin y. (5)
Pour un nombre complexe arbitraire, x+iy, on utilise aussi la relation
fondamentale (3) :
ex+iy =ex(cos y+isin y).
Exemples
•Un capital Cinvesti à un taux annuel de 3% deviendra, à la fin de
l’année,
C1 + 3
100 = 1,03C.
Si cependant l’intérêt est composé aux six mois, il deviendra
C1 + 3
200 2
= 1,03038C
et si l’intérêt est composé à chaque mois, il deviendra
C1 + 3
1200 12
= 1,03042C.
Si l’intérêt est composé « continûment », il deviendra, après un an
Ce0.03 = 1,03045C
et après tannées
Ce0,03t.
3

•Lorsque l’entier nest grand, on peut approximer n!à l’aide de la
formule de Stirling :
n!≈√2πn n
en
.
•Le nombre complexe
e2+3i=e2(cos 3 + isin 3) = 20,0855(−0,989 + 0,141i)
a pour module 20,0855.
Exercices
1. Calculer e50
505et e50 507.
2. Déterminer la partie réelle et le module des nombres complexes
e1+iπ et e−iπ/2.
Pour en savoir plus
?http://c.caignaert.free.fr/chapitre11/node5.html
?http://fr.wikipedia.org/wiki/Portail:Mathématiques
Réponses
1. 1,7×1013,6.6×1092. −e, e, 1,0
4