l`indispensable mathématique pour les études en physique

L’INDISPENSABLE MATHÉMATIQUE
POUR LES ÉTUDES EN PHYSIQUE

Collection « Cours et Manuels »
Harmattan Cameroun
Sous la direction de Roger MONDOUE
et Eric Richard NYITOUEK AMVENE
La plupart des élèves et étudiants africains achèvent leur cycle
d’apprentissage sans avoir accès directement aux sources des savoirs reçus. Les
cours et/ou manuels de leurs enseignants sont alors les seuls ou rares outils
pédagogiques disponibles. Il devient donc urgent de publier et diffuser ces cours
et manuels, afin d’assurer l’accès du plus grand nombre d’apprenants à une
éducation de qualité.
La collection Cours et Manuels est ouverte aux enseignants de toutes les
disciplines de l’enseignement maternel, primaire, secondaire et universitaire,
dont le souci majeur est de relever le niveau d’éducation et de promouvoir le
développement tant escompté sur le sol africain.
Déjà parus
François FOTSO, De la pédagogie par objectifs à la pédagogie des
compétences, 2011.
Joseph TANGA ONANA, Dissertation et commentaire en histoire, 2010.
Oscar ASSOUMOU MENYE, Mathématiques financières, outils et
applications, 2010.

Emire MAGA MONDESIR
Eliézer MANGUELLE DICOUM
Gilbert MBIANDA
L’INDISPENSABLE MATHÉMATIQUE
POUR LES ÉTUDES EN PHYSIQUE
Premier cycle universitaire
De l’angle au champ

© L’Harmattan, 2011
5-7, rue de l’Ecole-Polytechnique, 75005 Paris
http://www.librairieharmattan.com
[email protected]
[email protected]
ISBN : 978-2-296-54613-4
EAN : 9782296546134

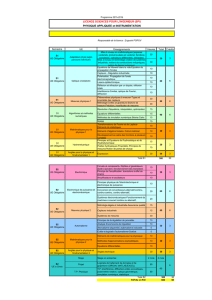
Table des matières
AVANT PROPOS xiii
I GEOMETRIE ET TRIGONOMETRIE 1
1 FORMES GEOMETRIQUES COURANTES 3
1.1 AIRES .................................. 3
1.2 VOLUMES ............................... 4
2 GEOMETRIE ELEMENTAIRE 5
2.1 L’ANGLE ................................ 5
2.1.1 DEFINITIONS ......................... 5
2.1.2 UNITES D’ANGLE ...................... 6
2.1.3 PROPRIETES CARACTERISTIQUES ........... 8
2.2 LE TRIANGLE ............................. 10
2.2.1 DEFINITIONS ......................... 10
2.2.2 DROITES REMARQUABLES DU TRIANGLE ...... 11
2.2.3 PROPRIETES ......................... 12
2.3 TRIANGLES PARTICULIERS .................... 15
3 TRIGONOMETRIE ELEMENTAIRE 17
3.1 ANGLE ORIENTE ........................... 17
3.2 CERCLE TRIGONOMETRIQUE .................. 18
3.3 APPLICATION AU TRIANGLE ................... 19
3.3.1 TRIANGLE QUELCONQUE . . .............. 19
3.3.2 TRIANGLE RECTANGLE,( Fig. 4),(illustration 5 page 168) 19
3.4 FORMULES TRIGONOMETRIQUES ................ 21
v