CHAPITRE 1 - MATHEMATICA FORTIS

CHAPITRE : Repérage dans le plan
I. Repère et coordonnées
Définition 1 : Un repère orthogonal du plan
est défini par trois points (O ; I, J) formant
un triangle rectangle de sommet O.
On a donc
Définition 2 : Un repère orthonormé du
plan est défini par trois points (O ; I, J)
formant un triangle rectangle isocèle de
sommet O.
On a donc
Remarque : La notation (O ; I, J) signifie :
Remarque : Un repère est un repère .
Propriété 1 (admise) : Dans un repère orthogonal, tout point M du plan est repéré par un
unique couple ( ; ) de réels appelé couple de coordonnées de M.
 est
 est
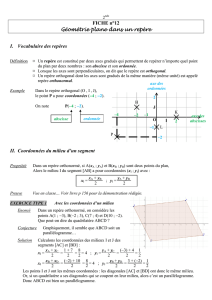
Exemple 1 :
Placer dans un repère orthonormé (O ; I, J),
les points A, B, C et D de coordonnées respectives
(3 ; 1), (-1 ; 4), (0 ; 4) et (2 ; 0).
Exemple 2 :
Placer dans un repère orthogonal (O ; I, J), avec OI = 4 cm et OJ = 2 cm
les points A, B, C et D de coordonnées respectives
(2 ; 1), (1 ; 2), (1 ; 1) et (-1 ; 2).
Axe des abscisses
Axe des abscisses
Axe des ordonnées
Axe des ordonnées
Origine du repère
Origine du repère

Exemple 3 :
Dans le repère (O ; I , J) ci-dessous, lire les coordonnées des points O, I, J, K, H, M, L et P.
II. Distance entre deux points du plan
Propriété 2 : Dans un repère orthonormé, A() et B( ; ) sont deux points du plan.
On a alors :
AB² =    
C’est-à-dire, la distance entre les points A et B est :
AB =    
Démonstration :
Outils : "le théorème de Pythagore"
Exemple 4 :
Dans un repère orthonormé A et B sont des points de coordonnées respectives (2 ; 8) et
(4 ; -2).
Quelle est longueur du segment [AB] ?

III. Milieu d’un segment
Propriété 3 : Dans un repère orthogonal, A(; ) et B(; ) sont deux points du plan.
Le milieu K du segment [AB] a pour coordonnées (,) avec :
= 
 et = 
Démonstration :
On procède par disjonction de cas :
1er cas : xA = xB ou yA = yB.
2ème cas : xA  xB et yA  yB.
Outils : "théorème des milieux"
Exemple 5 :
Dans un repère orthonormé A et B sont des points de coordonnées respectives (2 ; 8) et
(4 ; -2).
Quelles sont les coordonnées du point milieux C du segment [AB] ?

IV. Algorithme et repérage
Définition : Un algorithme est une suite finie d’instructions à appliquer dans un ordre
déterminé à un nombre fini de données pour arriver, en un nombre fini d’étapes, à un certain
résultat.
Exemple 6 :
Variables:
xA, yA , xB, yB, L
début algorithme:
Affecter une valeur à la variable xA
Affecter une valeur à la variable yA
Affecter une valeur à la variable xB
Affecter une valeur à la variable yB
L prend la valeur    
Afficher le message :
Afficher la valeur de L
Fin algorithme
Faire fonctionner cet algorithme pour :
 xA=2 ; yA=-3 ; xB=-1 ; yB=1
puis pour
 xA=5 ; yA=2 ; xB=-3 ; yB=1
C’est le cœur de l’algorithme.
C’est la sortie de l’algorithme.
Ce sont les variables de l’algorithme.

2 3 4 5 6 7 8 9-1-2-3-4-5-6-7-8-9
2
3
4
5
6
-1
-2
-3
-4
-5
-6
0 1
1
x
y