QCM de Maths

CљюѠѠђ : ₁_S₂JђѢёі ₀₅ ѓѼѣџіђџ ₂₀₁₅, ₂₃:₀₂
Élève fictif QCM de
Mathématiques
Durée : 0 min 34 s
Questions traitées : 9/10
Code du QCM : NDMJH Réponses justes : 6/10
Réponses fausses : 3/10
Barème : +1 / -0,2 Note : 10,80 / 20
1) Lʹaffirmation suivante : ʺSi est une fonction strictement décroissante sur un intervalle , alors
pour tout ʺ est :
Réponse n°1 : Réponse n°2 :
vraie fausse
2) Soit la courbe de la fonction racine carrée. La tangente à en son point dʹabscisse a pour
équation :
Réponse n°1 : Réponse n°2 : Réponse n°3 :
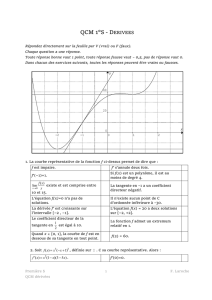
3) On considère la fonction définie sur et représentée par la courbe sur le graphique
ci-contre. On a construit deux tangentes à . La seule égalité vraie est :
Réponse n°1 : Réponse n°2 : Réponse n°3 :
4) Le nombre dérivé de la fonction inverse en est :
Réponse n°1 : Réponse n°2 : Réponse n°3 : Réponse n°4
:
5) Soit un réel. On considère la fonction . La fonction est
strictement décroissante sur si :
Réponse n°1 : Réponse n°2 : Réponse n°3 : Réponse n°4
:
6) Soit une parabole dont la tangente en son point dʹabscisse est parallèle à la droite
. Une équation de peut être :
Réponse n°1 : Réponse n°2 : Réponse n°3 :
Généré par Élève fictif - code QCM : NDMJH - Jeudi 05 février 2015, 23:02
f
I
x∈I,f(x) < 0
C
C
16
x
−
4
y
=
0
x
−
8
y
−
16
=
0
x
−
8
y
+
16
=
0
f
R
+
C
C
(0) = 2f
′
(1) = 0f
′
(1) = 1f
′
x↦
1
x
a= −
2
3
−
3
2
1
,
5
−
4
9
−
9
4
a
f:x∈
R
↦a−6 +ax + 4
x
3
x
2f
R
a∈[−2 ; 2 ]
3
√
3
√a∈]−∞ ; −2 ]∪[2 ; +∞ [
3
√
3
√a
⩽
−2
3
√a
⩾
2
3
√
P
−
2
∆ : x−y+ 3 = 0
P
y= − x− 1
1
4
x
2
3
2
y= − − x+
1
3
x
2
1
3
11
3
y= − 3x− 7
x
2

Généré par Élève fictif - code QCM : NDMJH - Jeudi 05 février 2015, 23:02
7) Soit . Le taux de variation de entre et est donné par :
Réponse n°1 : Réponse n°2 : Réponse n°3 :
8) On considère la fonction définie sur et représentée par la courbe sur le graphique
ci-dessous. On a construit deux tangentes à . Soit la fonction définie sur par .
Alors :
Réponse n°1 : Réponse n°2 : Réponse n°3 :
9) Soit une fonction définie et dérivable sur . On donne ci-dessous la représentation graphique
de sa fonction dérivée . La tangente à la courbe de en son point dʹabscisse a pour coefficient
directeur :
Réponse n°1 : Réponse n°2 : Réponse n°3 : Réponse n°4
:
10) Soient un entier naturel non nul et . Alors, pour tout ,
est égal à :
Réponse n°1 : Réponse n°2 : Réponse n°3 :
f:x∈
R
↦ − + x+ 1
x
2f
1
1
+
h
−
−
h
h
2
−
1
−
h
−2 − h−
1
h
f
R
+
C
C
g
R
+
g(x) =
1
f(x)
(0) =
g
′3
4
(0) = −
g
′1
3(0) = −
g
′3
4
f
R
f
′
f
0
0
−
2
−
4
4
n
g:x↦( )
1
−
x
−
−
−
−
−
√
n
x∈ ] −∞ ; 1 [ (x)
g
′
n( )
1
−
x
−
−
−
−
−
√n−1 −n( )
1
−
x
−
−
−
−
−
√n−1 −
n
2
( )
1
−
x
−
−
−
−
−
√n−2