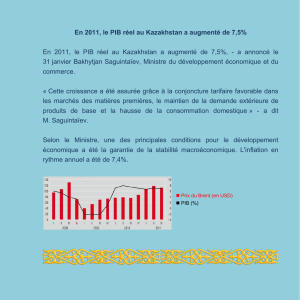
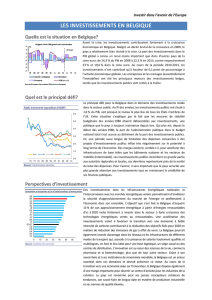
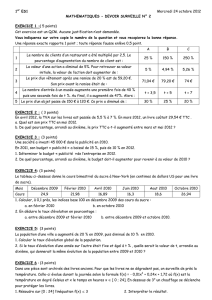
Modèle mathématique. Ne pas hésiter à consulter le fichier d`aide

1 ES1
DEVOIR A LA MAISON N°2
A rendre pour le ………………………………………………
EXERCICE 1 :
La société Pizzalo propose des pizzas à consommer sur place et d’autres à livrer. En janvier 2011, elle
a vendu pour 10 400 € de pizzas dans son restaurant et pour 23 000 € de pizzas avec son service de
livraisons.
1. Quel pourcentage du chiffre d’affaire représente en janvier la vente sur place.
2. En février, la vente sur place a baissé de 12% et la vente par livraison a augmenté de 8 %.
a. Le chiffre d’affaire a-t-il augmenté ? Justifier
b. Déterminer le pourcentage d’évolution du chiffre d’affaire.
c. Quel pourcentage du chiffre d’affaire représente en février la vente sur place.
3. Les bénéfices sont de 7 % sur une pizza vendue sur place et de 3 % sur une pizza livrée.
Déterminer le bénéfice de la société en janvier et en février, puis le pourcentage de variation du
bénéfice entre ces 2 mois.
EXERCICE 2 :
Une entreprise décide d’investir dans la publicité pour relancer ses ventes. On constate que le chiffre
d’affaire en euros correspondant à la somme x (en €) investie dans la publicité est donné par la
fonction f définie sur [0 ;10 000] par : f(x) = - 0,001x2 + 12,5x + 15 000
Les contraintes financières de l’entreprise lui imposent un chiffre d’affaire minimal de 45 000 €.
1. a. Résoudre l’inéquation f(x) ≥ 45 000
b. En déduire les sommes, arrondies à l’euro près, que l’entreprise peut investir dans la publicité ?
2. Quel est le montant, en euros, de l’investissement dans la publicité que l’entreprise n’a pas besoin
de dépasser. Justifier votre réponse.

CORRIGE DU DEVOIR A LA MAISON N° 2
EXERCICE 1 :
1. 10 400
10 400 + 23 000 = 10 400 33 400 0,311 = 31,1 %
En janvier la vente sur place représente environ 31,1 % de la vente totale.
2. a. 10 400 x 0 ,88 = 9152 23 000 x 1,08 = 24 840.
En février, la vente sur place rapporte 9152 € et la vente par livraison 24 840 €.
9 152 + 24 840 = 33 992 33 992 > 33 400 .
Le chiffre d’affaire est passé de 33 400 € à 33 992 € : il a donc augmenté.
b. VF – VI
VI = 33 992 – 33 400 33 400 0, 018 = 1,8%
Le chiffre d’affaire à augmenté d’environ 1,8%.
c. 9 152
33 992 0,269 = 26,9 %
En Février, la vente sur place représente environ 26,9 % de la vente totale.
3. 10 400 x 7
100 + 23 000 x 3 100 = 1418 9 152 x 7 100 + 24 840 x 3 100 = 1385, 84.
En janvier le bénéfice était de 1 418 € et en février de 1 385, 84 €
1385,84 – 1418
1418 - 0,023 = - 2,3 % .
Le bénéfice a baissé de 2,3% entre janvier et février.
EXERCICE 2 :
1. f(x) ≥ 45 000 – 0,001x2 + 12,5x + 1500 ≥ 45 000
– 0,001x2 + 12,5x – 3000 ≥ 0
On étudie donc le signe du trinôme – 0,001x2 + 12,5x – 3000 sur l’intervalle [0 ; 10 000]
= (12,5)2 – 4x(-0,001) x (-30 000) = 36,25 donc le trinôme a deux racines :
x1 =
0,002
36,2512,5
3 240 et x2 =
0,002
36,2512,5
9 260
a = - 0,001 < 0 donc – 0,001x2 + 12,5x – 30 000 ≥ 0 pour x ∈ [ 3240 ; 9260]
L’entreprise peut donc investir entre 3240 € et 9260 € dans la publicité tout en respectant
les contraintes financières.
2. f est une fonction polynôme du second degré. = -b
2a = - 12,5 -0,001 = 6250.
a < 0 donc la fonction f atteint son maximum en = 6250.
Cela signifie que pour l’entreprise, il est inutile de dépenser plus de 6 250 € en publicité.