Couple acide-base : CORRECTION

Page 1
CORRECTION DES EXERCICES DU CHAPITRE n° 4
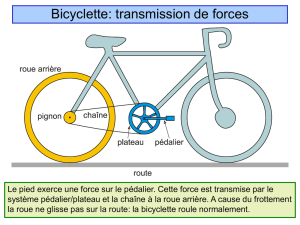
I) Cinématique du cycliste.
a) Lorsque le pédalier fait un tour, la chaîne avance de n2 crans ainsi que le pignon arrière qui
est entraîné par la chaîne.
Le pignon fait donc n2/n1 tours quand le pédalier fait 1 tour. La roue étant solidaire du pignon
arrière va faire également n2/n1 tours et le vélo va avancer d'une distance de 2.π.R.(n2/n1).
Le développement est : D = 2.π.R. 1
2
n
n
Pour n2 = 51 et n1 = 13, on a DM = 8,38 m
Pour n2 = 51 et n1 = 16, on a D = 6,81 m
Pour n2 = 51 et n1 = 18, on a D = 6,05 m
Pour n2 = 51 et n1 = 21, on a D = 5,19 m
Pour n2 = 51 et n1 = 25, on a D = 4,36 m
Pour n2 = 41 et n1 = 13, on a D = 6,74 m
Pour n2 = 41 et n1 = 16, on a D = 5,47 m
Pour n2 = 41 et n1 = 18, on a D = 4,87 m
Pour n2 = 41 et n1 = 21, on a D = 4,17 m
Pour n2 = 41 et n1 = 25, on a Dm = 3,50 m
b) Pour obtenir la plus petite vitesse de rotation du pédalier pour une vitesse de translation
donnée (v = 36 km.h−1 = 10 m.s−1, il faut choisir le plus grand développement.
La vitesse de translation du cycliste est alors donnée par : v = DM/∆t [1] où ∆t est la durée
(inconnue) pour parcourir la distance DM à la vitesse de mesure v.
Quand le cycliste parcourt une distance égale à DM le pédalier fait 1 tour d'après le a) : la
vitesse angulaire du pédalier est donc : ωm = 1/∆t [2] (en tr/s).
En éliminant ∆t entre les équations [1] et [2], on obtient :
ωm =
M
D
v
= 38,8
10
= 1,19 tr.s−1
c) Pour obtenir la plus grande vitesse de rotation du pédalier pour une vitesse de translation
donnée (v = 36 km.h−1 = 10 m.s−1, il faut choisir le plus petit développement.
ωM =
m
D
v
= 50,3
10 = 2,86 tr.s−1
II) Vitesse linéaire, vitesse angulaire.
a) La relation entre la vitesse angulaire ω et la mesure v de la vitesse linéaire d'un point mobile
en mouvement circulaire de rayon R est : v = R.ω =
TR..2 π
où T est la durée d'un tour.
Soit T =
vR..2 π
= 500 10.47,9.10.8,2..2 124
π ≈ 3,33.1015 s = 1,06.108 a
Rappelons que l'âge de l'Univers est estimé à 15 milliards d'années (1,5.1010 a) depuis le
"Big-Bang", que notre Galaxie s'est formée il y a environ 12 milliards d'années (1,2.1010 a) et
que le système solaire existe depuis près de 4,5 milliards d'années (4,5.109 a) : le Soleil
aurait donc déjà fait un peu plus de 40 fois (4,5.109/1,06.108) le tour de la Galaxie.
b) i. On a ω = 2
rv =
5,02
= 4 rad.s−1 = 0,64 tr.s−1
ii. Les deux poulies étant solidaires, elles tournent avec la même vitesse angulaire ω :
vA = ω.r1 = 4.0,2 = 0,8 m.s−1

Page 2
III) Mesure d'une masse.
a) Dans un référentiel (R), lié au laboratoire, le mobile est
soumis à trois forces :
- Son poids
→
P
= m.
→
g
, vertical dirigé vers le bas, P = m.g.
- La réaction
→
R
de la table horizontale, verticale (les
frottements étant négligeables) et dirigée vers le haut.
- la tension
→
F
du ressort, horizontale et toujours dirigée
vers l'axe de rotation.
Dans (R), la deuxième loi de Newton., nous donne :
→
P
+
→
R
+
→
F
= m.
→
a
b) On peut projeter cette équation vectorielle dans un repère tournant (repère de Frénet) :
- sur un axe vertical dirigé vers le haut : − P + R = 0 soit R = P
- sur un axe horizontal dirigé vers l'axe : F = m.a
Seule la tension du ressort contribue à la variation du mouvement.
Sous l'action de ces forces, le mobile a un mouvement circulaire (d'après l'énoncé).
→
F
, et donc,
→
a
sont dirigés vers le centre du cercle trajectoire, l’accélération est normale :
a = aN =
R
v
2
= ω2.R et aT =
dt
dv
= 0 d’où v = cte = v0 (en norme)
Le mobile a un mouvement circulaire uniforme.
c) 21 traces c'est-à-dire 20 intervalles font un angle de 135 °. par définition ω (en rad.s−1) :
ω0 = t.20
∆
α
=
3
106020180 xxx x
−
πα
= 1,97 rad.s−1
d) On a F = m.ω2.R d'où : m =
R.
F
2
ω
=
( )
150,097,1 35,0
x
2
= 0,601 kg
En bon accord avec la valeur donnée par la balance.
Remarque : la masse déterminée avec une balance, est liée à l'existence du champ de
pesanteur, on détermine donc de cette façon une masse "de gravitation"; la
masse déterminée dans ce mouvement de rotation n'est pas liée à l'existence
du champ de pesanteur, on détermine ici une masse "d'inertie".
En théorie il y a autant de différence entre ces deux types de masses qu'il
y a de différence entre la masse et la charge électrique. C'est l'égalité
entre les mesures de ces deux types de masses qui a permis à Einstein
de développer sa théorie de la relativité générale.