Lois et théorèmes des circuits

GEL-21945
Circuits
LOIS ET THÉORÈMES DE CIRCUITS

Objectifs
• comprendre et être capable d’utiliser les lois de Kirchhoff;
• reconnaître les éléments en série ou en parallèle dans un circuit
complexe;
• obtenir les dipôles équivalents d’éléments en série ou en parallèle;
• calculer correctement des diviseurs de tension ou des diviseurs de
courant simple ou en cascade;
• savoir mettre à zéro (annuler) une source de tension ou de courant;
• savoir transformer un circuit électrique complexe en son équivalent
Thévenin et son équivalent Norton
• être capable de passer d’un équivalent Thévenin à un équivalent
Norton et vice-versa;
• utiliser un équivalent Thévenin ou Norton entre deux bornes d’un
circuit pour déduire la tension ou le courant par ces bornes;
• comprendre clairement ce que signifie un système linéaire avec ses
avantages;
• exploiter les caractéristiques d’un système linéaire dont le principe
de superposition des sources. 2/73

Plan du cours
Lois de Kirchhoff
Dipôles équivalents
Transformations de sources
Théorèmes de Thévenin et de Norton
Transfert maximal de puissance
Principe de superposition
3/73

+
-
v
a b c
d
e f
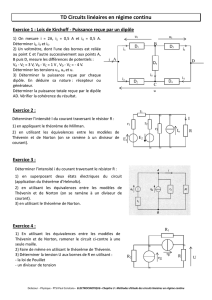
- Une jonction où au moins deux éléments électriques ont une connexion
commune est appelée nœud
- Dans chaque élément, on peut définir une variable tension v et une
variable courant i
Noeuds
Éléments
Parcours fermés
a-b-c-d-e-f-a
a-b-e-f-a
b-c-d-e-b
Éléments, nœuds et parcours fermés
4/73

Lois de Kirchhoff
5/73