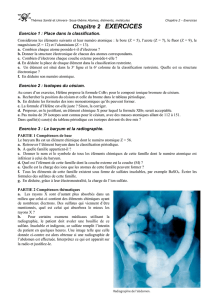
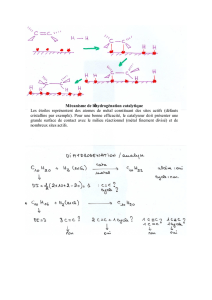
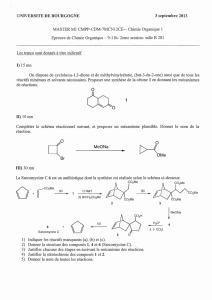
DST 5

CLASSE DE PREMIÈRE S
Le : 14 janvier 2009
Durée : 2 h 00
DEVOIR SUR TABLE N° 5
TOUT DOCUMENT INTERDIT.
L’usage de calculatrices scientifiques à mémoire est autorisé.
Les résultats numériques doivent être précédés d’un calcul littéral.
La présentation et la rédaction font partie du sujet et interviennent dans la notation.
L’épreuve est notée sur 16 points auxquels s’ajouteront les points d’épreuve pratique sur 4 points.
I ] CHIMIE : sur 8 points. IDENTIFICATION DES I
IDENTIFICATION DES IIDENTIFICATION DES I
IDENTIFICATION DES IONS SULFATE
ONS SULFATEONS SULFATE
ONS SULFATE
L’identification des ions sulfate se fait par précipitation du sulfate de baryum, BaSO4 (s), grâce à une solution de
chlorure de baryum, Ba2+
aq + 2 Cl– aq.
À 20,0°C, on ajoute, à V3 = 100 mL d’eau distillée, un volume : V1 = 100 mL d’une solution aqueuse S1 de chlorure de
baryum de concentration molaire volumique en soluté apporté : C1 = 5,00.10-3 mol.L-1. On verse alors dans le mélange
précédent un volume : V2 = 200 mL d’une solution aqueuse S2 de sulfate de sodium, 2 Na+
aq + SO4
2–
aq, de concentration
molaire volumique en soluté apporté égale à : C2 = 8,00.10-3 mol.L-1.
1. La solution S1 de chlorure de baryum a été préparée à partir d’une solution mère S0 décimolaire.
Décrire, sous forme de schémas légendés, la méthode de préparation de la solution S1.
2. Dessiner un modèle de structure pour le chlorure de baryum solide, en supposant qu’il cristallise dans le même
système cubique que le fluorure de calcium, CaF2.
3. Qu’observe-t-on dans le milieu réactionnel lors de l’ajout de la solution S2 ?
4. L’équation chimique modélisant la réaction chimique se produisant lors de l’ajout de la solution S2 s’écrit :
2 Na+
aq + SO4
2–
aq + Ba2+
aq + 2 Cl– aq →
→→
→ BaSO4 (s) + 2 Na+
aq + 2 Cl– aq
4.1. Calculer les quantités de matière initiales des réactifs.
4.2. Construire le tableau d’avancement de la transformation chimique qui se produit.
4.3. Déterminer la valeur de l’avancement maximal de cette transformation chimique.
4.4. Établir le bilan des quantités de matière des espèces chimiques présentes dans le milieu réactionnel à l’issue de
cette transformation.
4.5. Calculer les concentrations molaires volumiques des espèces chimiques dissoutes dans le milieu réactionnel à
l’issue de la transformation.
5. On mesure, à 20,0°C, la conductance G du mélange réactionnel après réaction. On utilise pour cela une cellule
conductimétrique constituée de deux plaques métalliques de 1,00 cm2 de section et distantes de 15,0 mm. La mesure
fournit : G = 0,700 mS.
5.1. Faire un schéma légendé du montage utilisé pour réaliser cette mesure de conductance.
5.2. Déterminer une valeur expérimentale de la conductivité σ
σσ
σ du mélange testé.
5.3. Pour quelle raison doit-on préciser la température du milieu réactionnel ?
6. La valeur de la conductivité du milieu réactionnel testé peut être déterminée par calcul, avec la connaissance des
valeurs des conductivités molaires ioniques des ions en présence.
6.1. Calculer une valeur numérique de la conductivité σ
σσ
σTh du milieu testé.
6.2. Comparer les valeurs obtenues pour σ
σσ
σ et σ
σσ
σTh. Déterminer un pourcentage d’écart.
6.3. Donner deux causes d’erreurs de mesures qui pourraient expliquer la différence observée ?
Données : Conductivités molaires ioniques à 20,0°C :
λ
λλ
λNa+ = 50,1.10-4 uSI ; λ
λλ
λCl– = 76,3.10-4 uSI ; λ
λλ
λBa 2+ = 127.10-4 uSI ; λ
λλ
λSO4 2– = 160.10-4 uSI.
... / ...

II ] PHYSIQUE : sur 8 points. LA M
LA MLA M
LA MONTÉE
ONTÉE ONTÉE
ONTÉE D’UNE
D’UNE D’UNE
D’UNE CÔTE
CÔTECÔTE
CÔTE
Un véhicule automobile, assimilé à son centre d‘inertie G, de masse : M = 1,20 tonnes, monte, à la vitesse constante
VG = 72,0 km.h-1, une côte inclinée de : α
αα
α = 10,0° sur l’horizontale. On prendra : g = 9,81 m.s-2.
1. Énoncer la condition d’équilibre d’un système matériel.
2. La force d’action de l’air sur le véhicule,
f
air, est opposée au vecteur vitesse
V
G de son centre d’inertie. Sa norme,
fair, est proportionnelle au carré de la valeur VG de sa vitesse. La constante de proportionnalité, notée k, s’exprime par :
k = 0,5.Cx.ρ
ρρ
ρ air.S, où :
 0,5 est un facteur sans unités ;
 Cx est un coefficient caractérisant la forme plus ou moins aérodynamique du véhicule, on prendra : Cx = 0,350 ;
 ρ
ρρ
ρ air est la masse volumique de l’air, on donne : ρ
ρρ
ρ air = 1,30 kg.m-3 ;
 S est la surface frontale que présente le véhicule à l’air, on donne : S = 5,00 m2.
Pour simplifier l’étude, on supposera que les actions de frottement de freinage entre les pneumatiques
et la chaussée n’interviennent pas.
2.1. Exprimer, puis calculer, la valeur de fair.
2.2. Quelle est l’unité de Cx ?
3. La force d’action de la chaussée sur le véhicule possède une composante perpendiculaire à
V
G, notée R
.
Déterminer l’expression littérale en fonction des données, puis donner la valeur numérique, de la norme R de R
.
4. Quelle doit être la valeur numérique de la norme F de la force de propulsion F du véhicule pour maintenir constante
la valeur VG de sa vitesse ?
5. La force de propulsion, F
, se répartit également sur les deux roues avant du véhicule. On appelle coefficient de
frottement, noté f, le rapport de la force de propulsion, pour une roue motrice, à la composante perpendiculaire à
V
G de
l’action de la chaussée, ramenée à une roue. Déterminer une valeur numérique de f.
6. Le véhicule gravit la distance rectiligne AB = 500 m sur la côte inclinée.
6.1. Exprimer, puis calculer numériquement, le travail mécanique de la force de propulsion F
au cours du
déplacement AB
.
6.2. Que vaut la puissance mécanique instantanée de F
?
6.3. Exprimer, puis calculer numériquement, le travail mécanique du poids du véhicule au cours du même
déplacement AB
.
6.4. Exprimer, puis calculer numériquement, le travail mécanique de la force
f
air au cours du déplacement
A
B
.
6.5. Que vaut la somme algébrique des travaux des forces appliquées au véhicule au cours du déplacement
A
B
 ?
7. Arrivé en B, le conducteur coupe brutalement et instantanément le moteur.
7.1. Énoncer la deuxième loi de Newton.
7.2. Déterminer la direction et le sens de la résultante des forces d’action subies par l’automobile, dans ces
nouvelles conditions.
7.3. Que devient alors le vecteur vitesse
V
G du véhicule ?
On précisera sa direction, son sens et l’évolution de sa norme.