Résolution des systèmes optiques et Maple

Vol. 95 - Juin 2001 Roland BOUFFANAIS
BULLETIN DE L’UNION DES PHYSICIENS 1003
Résolution des systèmes optiques
et Maple
par Roland BOUFFANAIS
Professeur de physique-chimie en PT
25, Leonie Hill Road
# 2202 Grangeford - Singapore 239196
[email protected]
RÉSUMÉ
Nous nous proposons dans cet article d’illustrer l’utilisation du logiciel MAPLE en
complément des travaux pratiques d’optique. Ce logiciel permet de simuler des situations
physiques difficilement réalisables en pratique ; des simulations peuvent aider les élèves
à mieux comprendre les phénomènes qu’ils étudient.
Deux situations sont envisagées dans cet article :
– la visualisation du phénomène de limite de résolution des instruments d’optique due à
la diffraction et la définition d’un critère équivalent au critère de RAYLEIGH pour définir
cette limite ;
– l’influence du nombre Nde motifs constituant un réseau sur le pouvoir de résolution
de ce dernier.
1. LIMITE DE RÉSOLUTION D’UN INSTRUMENT D’OPTIQUE
Trois facteurs influencent la résolution d’un instrument d’optique (lunette astrono-
mique, télescope, appareil photographique, etc.) : le stigmatisme du système optique le
constituant, l’acuité du récepteur d’images et la diffraction. Notre étude se limitera à l’in-
fluence de la diffraction et nous supposerons le système optique rigoureusement stigmatique.
L’instrument étant d’extension finie, il limite l’onde reçue depuis l’objet et diffracte
cette dernière. A chaque objet supposé ponctuel (étoile lointaine par exemple) correspond
une tache image centrée sur l’image géométrique.
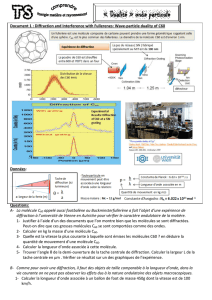
1.1. Diffraction par une pupille circulaire
La première étape de notre étude est d’étudier la tache de diffraction obtenue par
diffraction d’une onde plane à travers une pupille circulaire (symétrie de révolution des
instruments d’optique).

BULLETIN DE L’UNION DES PHYSICIENS
1004
Résolution des systèmes optiques et Maple BUP no835
L’application du principe d’HUYGENS-FRESNEL dans le cadre de la diffraction de
FRAUNHOFER (formation des images) donne l’intensité Idiffractée dans une direction
définie par le rayon angulaire
i
, pour une pupille circulaire de diamètre
DR2=
(cf.
figure 1). Cette pupille représente le diaphragme d’ouverture de l’instrument d’optique
étudié. L’intensité sur l’écran est identique à celle du montage suivant (cf. figure 2) qui
correspond à la formation de l’image d’un point objet à distance finie.
Figure 1 : Observation de la diffraction de FRAUNHOFER due a une pupille circulaire.
Figure 2 : Formation de l’image d’un point source à distance finie.
La symétrie de révolution du système optique impose à l’intensité Ide ne dépendre
que de
i
; son calcul fait apparaître la fonction de BESSEL d’ordre 1
()Jx
1
:
() /
(/)
sin
sin
II R
JR
42
2
01
2
=irim
rim
J
L
K
K
N
P
O
O
I
0
étant l’intensité maximale au niveau de l’image géométrique. En pratique, l’angle
i
sera faible et nous prendrons
sin -ii
.
Les commandes MAPLE suivantes permettent de tracer cette fonction de la variable
i
(on prend
/R21=m
et
/I14
0=
pour ce tracé) :
> with(plots):
> i:=(BesselJ(1,Pi*theta)/(Pi*theta))^2;
:(, ) i1BesselJ
22
2
=ri
ri
> plot(i,theta=–4..4);
La fonction de BESSEL d’ordre 1
()Jx
1
est intégrée à MAPLE par le biais de la com-
mande
BesselJ(1,x) (cf. figure 3).
Remarquons que la largeur angulaire de la tache centrale qui est de loin la plus
lumineuse, est
,122=iD
en variable réduite soit
,/D122=imD
. Ce résultat générale-
ment admis est ici vérifié graphiquement.

Vol. 95 - Juin 2001 Roland BOUFFANAIS
BULLETIN DE L’UNION DES PHYSICIENS 1005
Néanmoins le graphe précédent n’est pas représentatif de ce qui est observé en pra-
tique sur un écran ou bien directement à l’œil. En effet l’observation donne une image
plane bidimensionnelle où l’intensité en tout point est donnée par le graphe précédent.
Pour simuler à l’aide de MAPLE ce qui est effectivement observé, nous procédons de la
façon suivante :
> with(plots):
> i:=(BesselJ(1,Pi*sqrt(x^2+y^2))/(Pi*sqrt(x^2+y^2)))^2;
:()
,
ixy
xyBesselJ 1
22 2
22
2
=+
+
r
r
ak
> contourplot(i,x=-3..3,y=-3..3,filled=true, coloring=[white,bluel,
> contours=[0.001,0.003,0.008,0.012,0.016,0.02],grid=[100,100]);
Dans la simulation précédente la variable angulaire
i
a été remplacée par la variable
linéaire radiale
rxy
22
=+
. Ce changement de variable ne pose aucun problème si nous
n’oublions pas que nous travaillons avec des variables réduites, en effet :
sin tan L
r
L
xy
et 22 ---=+ ii ii
la distance Létant définie sur les figures 1 et 2. En variable réduite, nous prenons
L1=
.
La commande MAPLE
contourplot(i,...) à la base de ce graphe représente les
Figure 3 : Tracé de la fonction de BESSEL d’ordre 1 par MAPLE.

BULLETIN DE L’UNION DES PHYSICIENS
1006
Résolution des systèmes optiques et Maple BUP no835
lignes de niveau de la fonction iassociée à l’intensité lumineuse I. Le dégradé de gris est
rendu proportionnel à l’intensité lumineuse au point de coordonnées (x, y) à l’aide de
l’option
coloring . L’option grid quant à elle définit le pas de la grille de calcul dans le
plan du graphe.
L’option
contours est fondamentale pour la commande contourplot ; elle permet de
choisir la valeur de la « ligne de niveau »
I Cte=
à tracer. Le choix de ces valeurs est sug-
géré par l’allure de l’intensité tracée précédemment pour observer les anneaux concen-
triques et non pas uniquement la tache centrale, il faut prendre des contours de valeur
inférieure à 0,05.
Sur la figure 4, nous retrouvons bien les caractéristiques de la tache d’AIRY : une
tache centrale très lumineuse, centrée sur l’image géométrique et entourée d’anneaux
concentriques d’intensité moindre.
1.2. Observation de deux sources lumineuses incohérentes
de même intensité
1.2.1. Figure de diffraction
En supposant l’objet ponctuel, nous venons de voir que l’image de ce point est une
tache. Deux points objets voisins donnent deux taches, qui s’ajoutent en intensité car il
s’agit d’objets incohérents. L’écart angulaire
f
entre ces deux objets ponctuels est alors
le paramètre fondamental de notre étude. Simulons à l’aide de MAPLE deux situations
Figure 4 : Simulation de la tache de diffraction due à une pupille circulaire.

Vol. 95 - Juin 2001 Roland BOUFFANAIS
BULLETIN DE L’UNION DES PHYSICIENS 1007
limites correspondant aux deux situations physiques suivantes :
♦Pour de grandes valeurs de
f
les deux taches images sont distinctes, les deux objets
sont résolus par le système optique. Nous retrouvons avec MAPLE cette situation en
prenant
,15=f
(cf. figure 6) dans nos variables réduites (1).
> with(plots):
> i:=(x,y)->(BesselJ(1,Pi*sqrt(x^2+y^2))/(Pi*sqrt(x^2+y^2)))^2;
:(,) , ixy
xy
xy1BesselJ
222
2
22
2
"=
+
+
r
r
ak
> contourplot(i(x,y)+i(x-1.5,y-1.5),x=-5..5,y=-5..5,filled=true,
> coloring=[white,blue],
> contours=[0.001,0.003,0.008,0.012,0.016,0.02],grid=[100,100]);
Figure 5 : Diffraction par une pupille circulaire avec deux sources incohérentes.
Figure 6 : Simulation de la tache de diffraction avec
,15=f
.
(1)
/rL
0
==if
est la position de l’image désaxée.