UE103 – Optique géométrique - Devoir surveillé N°2

UE103 – Optique géométrique - Devoir surveillé N°2 - 02/11/07 1/6
Université Pierre et Marie Curie - LP1 - UE 103 - Année 2004-2005
Optique géométrique - Devoir surveillé N°2
[email protected]
I) Etude des conditions de stigmatisme d’un miroir sphérique.
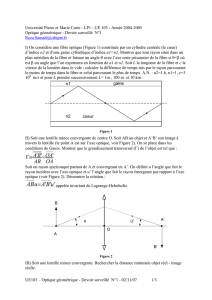
On considère un miroir sphérique concave (voir Figure 1) de rayon R, de centre C et de
sommet S.
a. Formuler la notion de stigmatisme rigoureux (ou exact).
b. Soit un objet A placé à l’infini sur l’axe optique. Y’a-t-il stigmatisme exact pour cet
objet vu à travers ce système optique ? Expliquer qualitativement pourquoi.
c. On considère un rayon issu de A, celui-ci est donc parallèle à l’axe optique. On
désigne par yi son ordonné. On note M l’intersection entre le rayon émergeant du
système et l’axe des abscisses. Soit enfin x l’abscisse du point M et i l’angle entre le
rayon incident et la normale à la surface au point I (voir Figure 1). Monter alors que
CM=R / (2 cos i) . Pour quelle condition sur i aura-t-on stigmatisme approché ?
d. Exprimer maintenant x en fonction de yi. Pour quelle condition sur yi a-t-on
stigmatisme (approché) ? Comment nomme-t-on cette condition ? Comment appelle-t-
on alors le point M et que vaut la focale du système ?
e. A quelle condition sur yi a –t-on stigmatisme à 10% près ?
C
Sx
i
I
y
yi
MH
Figure 1

UE103 – Optique géométrique - Devoir surveillé N°2 - 02/11/07 2/6
II) Catadioptre1 : On place un miroir plan dans le plan focal image d’une lentille convergente
de vergence D=0.1 dioptrie.
a. Montrer qu’un rayon lumineux ressort parallèlement à lui-même après avoir traversé
le système optique (lentille+miroir).
b. Trouver la position et la taille de l’image d’un objet placé dans le plan focal objet de la
lentille.
c. Donner la relation de conjugaison avec origine en F et le grandissement du système
étudié.
III) Un observateur emmétrope (i.e. ayant une vision normale) regarde à l’oeil nu un tout
petit objet plan que l’on assimile à un segment AB de longueur l orthogonal à l’axe optique
Ox. On note dm la distance minimale de vision distincte (le punctum proximum).
a. Déterminer l’angle um sous lequel est vu l’objet à l’oeil nu à la distance dm.
b. L’observateur regarde maintenant AB à travers une loupe (lentille mince convergente)
de distance focale f’ et de centre O. Son oeil est situé à distance a< dm de la loupe.
Déterminer les positions de l’objet rendant possible l’observation nette. Faire une
construction géométrique d’une telle image. L’image est-elle droite ou renversée ?
Est-elle réelle ou virtuelle ?
c. Pour quelle position l’observation se fait-elle sans fatiguer l’oeil ? Exprimer l’angle u’
sous lequel est vu l’objet dans ce cas. En déduire alors le grossissement commercial de
la loupe (Gc=u’/ um)?
1 Catadioptrique : Composé des deux mots catoptrique et dioptrique, et résumant les deux branches de la
physique, et plus spécialement de l'optique, qui ont pour objet l'étude de la réflexion de la lumière à la surface
des corps et l'étude de la transmission de la lumière au travers des corps transparents. La catadioptrique
s'applique à tout ce qui appartient à la fois à ces deux branches et particulièrement à l'étude des instruments
d'optique qui réunissent les effets combinés de la réflexion et de la réfraction.

UE103 – Optique géométrique - Devoir surveillé N°2 - 02/11/07 3/6
Solutions :
I) Dioptre sphérique
a) Stigmatisme rigoureux : on a stigmatisme rigoureux pour un objet A donné,
lorsque l’ensemble des rayons lumineux passent, après avoir traversé le système
optique, par un point unique appelé alors A’ image de A.
b) Non : Le point objet situé à l’infini n’admet pas de stigmatisme exact à travers le
système. En effet on montre par construction géométrique que des rayons
parallèles à l’axe optique ne convergent pas en un point unique après avoir
traversé le miroir sphérique.
c) La loi de la réflexion impose que l’angle CIM soit égal à l’angle d’incidence i. Par
conséquent on en déduit que le triangle CIM est isocèle. Soit N le projeté de M sur
le segment CI : puisque CIM est isocèle CN=CI/2=R/2. Par ailleurs CM=cos(i)CN
par conséquent CM=R/2/cos(i). On a stigmatisme (approché) pour un ensemble de
rayons tels que CM soit constant. Pour le rayon confondu avec l’axe optique : i=0
et CM=R/2. CM demeure alors constant et égal à R/2 lorsque cos(i) ~ 1 ce qui
est réalisé lorsque i demeure petit.
d) On a yi=R sin(i) d’où : yi²=R² ( 1 – cos² i) = R² [ 1 – (2 R/CM) ² ] . Il vient alors
la relation recherchée : CM= R /2 / [1 –(-yi/R)²]1/2. On a stigmatisme (approché)
lorsque CM~cte~R/2. Ce qui est réalisé lorsque yi<<R. Autrement dit les rayons
doivent demeurer peu éloignés de l’axe : cette condition est l’une des deux
conditions de Gauss. Le point M est alors l’image unique de l’objet placé à
l’infini : on le désigne alors par « foyer image » (F’).
e) On cherche un stigmatisme à 10% près. Autrement on veut que le point M soit à
10% près confondu avec le foyer image F’ : on veut donc que
γ ≤
−
CF
CFCM . avec
γ=10%.Ceci implique que : ²
)²/(1
)²/(
γ ≤
−Ry
Ry
i
isoit enfin ²1
γ
γ
+
≤R yi
II) Catadioptre :
a) Considérons le rayon quelconque (1) représenté sur la Figure 2. Pour en
déterminer le trajet à travers le système considérons le rayon (2) qui lui est
parallèle et qui passe par le foyer objet. Ce rayon sort de la lentille (L) en un rayon
parallèle à l’axe optique et rencontre le miroir au point N pour y être réfléchi en un
rayon à nouveau parallèle à l’axe. Après avoir traversé L, ce rayon ressort donc en
passant par le foyer F. Après sorti du système le rayon (2) reste donc confondu
avec lui même. Le rayon (1) étant parallèle à (2), il passe donc par le point N . Il
est réfléchi par le miroir en faisant un angle i avec l’axe optique (voir Figure 2) et
rencontre alors la lentille (L) au point M. En vertu du retour inverse le rayon qui
serait parallèle au rayon (2) et qui passerait par le point M, convergerait, après
avoir traversé L, vers le point N. En vertu du principe de retour inverse de la
lumière il existe un rayon lumineux (3) qui effectue le même trajet. Par
conséquent on conclue que le rayon NM ressort de la lentille sous forme du rayon
(3) parallèle au rayon (1), CQFD.
b) En vertu de ce qui précède, l’objet AB admet – par construction géométrique -
l’image A’B’ représentée sur la Figure 3. Le trajet du rayon (1) permet d’établir
que AB=-A’B’, autrement dit le grandissement est égal à -1.
c) L’image A’B’ d’un objet quelconque se construit en utilisant le trajet des deux
rayons (1) et (2) (voir Figure 4) : le rayon (1) permet d’établir que AB=-A’B’, le
rayon (2) permet d’affirmer que A’ est le symétrique de A par F, d’ou la relation
de conjugaison FA=-FA’
III ) La loupe

UE103 – Optique géométrique - Devoir surveillé N°2 - 02/11/07 4/6
a) L’objet est « petit » par conséquent um=l/dm.
b) On a A’O=D-a (voir Figure 5). Notons x=OA. La relation de conjugaison s’écrit
alors : ''
111
fxDa =− − , il vient alors l’expression Daf
fDa
x+−
−
='
')( . L’image, pour être
observée de manière nette, doit être telle que D≥ d
m. Le cas limite où D= d m
correspond à la valeur particulière
m
m
mdaf
fda
xx +−
−
== '
')( . La construction géométrique
permet d’établir que lorsque OA<OF=-f’, l’image est réelle (et inversée) et ne peut
pas être vu avec l’oeil. En revanche lorsque OF<OA, l’image est virtuelle et droite
(grandissement positif) comme le montre la Figure 5. On constate aussi géométrique
que lorsque A s’approche de O, la distance D décroît. Par conséquent D≥ dm implique
que : –f’ ≤ x ≤ xm.
c) L’image est observée sans fatiguer l’oeil lorsque celle-ci se situe à l’infini, ce qui se
réalise lorsque A est placé au foyer objet (voir Figure 6). L’angle u’ sous lequel
l’image correspondante est observée, est donc u’=l/f’. D’ou le grossissement
commercial : Gc≡ u’/um=dm /f’.
F
F’
(1)
(2)
i
i
(3)
M
N
Figure 2

UE103 – Optique géométrique - Devoir surveillé N°2 - 02/11/07 5/6
F
F’
B
A
B’
(1)
2i
2i
Figure 3
F
F’
(1)
(2)
B
A
B’
A’
Figure 4