Correction Exo Tour de Pise

Physique : 1S Approche des lois de Newton
Exercices d’application
Exercice 2 :
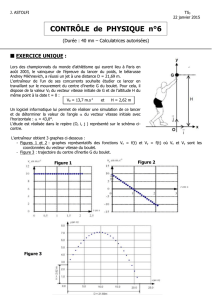
Le document ci-contre représente la chronophotographie
d’un boulet en hommage à l’expérience de Galilée.
Ce boulet de masse m = 1,0 kg et de volume V = 0,16 dm
3
est lâché sans vitesse initiale du dernier étage de la tour
de Pise à une date prise comme origine des temps.
L’intervalle de temps séparant deux positions consécutives
du boulet est ∆t = 0,50 s.
Donnée : ρ
air
= 1,3 kg.m
-3
1. Dans quel référentiel est étudié le mouvement du boulet ?
Le mouvement du boulet est étudié dans le référentiel
Terrestre supposé galiléen
2. Dresser le diagramme objet-interaction de la chute du boulet.
Le D.O.I de la situation :
3. Dresser le diagramme des actions mécaniques pour le système
{boulet}. Représenter ces forces sans tenir compte de l’échelle.
Le D.A.M pour le système <<Boulet>>
L’air exerce sur le boulet deux forces :
 La force de frottement  f opposée au mouvement dont la valeur est proportionnelle à
la vitesse du boulet
 La poussée d’Archimède  f
A
4. Montrer que l’on peut négliger la poussée d’Archimède f
A
par rapport au poids P.
P = mg soit P = 1,0 x 9,80 = 9,8 N
F
A
= ρ
ρρ
ρ
air
. V. g = 1,3 x 0,16 x 10
-3
x 9,80 = 2,0.10
-3
N
Comparaison :
P
f
A
= 9,8
2,0.10
-3
= 4,9.10
3
La valeur du poids est environ 5000 fois importante que celle de la poussée d’Archimède.
On peut alors négliger f
A
devant P.
On considère alors que les deux forces agissant sur le boulet sont le poids  P et la force de frottement
de l’air  f.
5. Déterminer l’échelle spatiale du document.
Echelle spatiale :
D’où : x = 1,0 x 50
8,5 = 5,9
1 cm sur la chronophotographie représente 5,9 m dans la réalité.
Il suffit donc de multiplier par 5,9 les mesures des distances en cm sur le document afin de
les convertir en longueurs réelles en m
Document (en cm) Réalité (en m)
8,5 50
1,0 x
Boulet
Terre
Air
Air Boulet Terre

6. Calculer les valeurs v(t
i
) de la vitesses instantanée du boulet aux instants t
2
, t
3
, t
4
, t
5
et t
6
.
Quelle conclusion peut-on en tirer concerna la somme vectorielle des forces agissant sur le boulet ?
Par définition, la vitesse instantanée v(t
i
) s’exprime par la relation suivante :
v(t
i
) = G
i-1
G
i+1
t
i+1
– t
i-1
Calculons les vitesses instantanées aux instants t
2
, t
3
, t
4
, t
5
et t
6
, à partir de la chronophotographie du boulet :
v(t
2
) = G
3
G
1
/2 ∆
∆∆
∆ t = 0,85
x 5,9
2 x 0,50 = 5,0 m.s
-1
v(t
3
) = G
4
G
2
/2 ∆
∆∆
∆ t = 10 m.s
-1
v(t
4
) = G
5
G
3
/2 ∆
∆∆
∆ t = 15 m.s
-1
v(t
5
) = G
6
G
4
/2 ∆
∆∆
∆ t = 20 m.s
-1
v(t
6
) = G
7
G
5
/2 ∆
∆∆
∆ t = 25 m.s
-1
Le boulet est lâché sans vitesse initiale :
A t
1
= 0 s v(t
1
) = 0 m.s
-1
7. Représenter le vecteur ∆ v (t
5
) = v (t
6
) - v (t
4
).
Quelle conclusion peut-on en tirer quant aux valeurs des deux forces appliquées au boulet ?
Pour représenter les vecteurs-vitesse, il faut choisir une échelle de vitesse.
Prenons comme échelle : 1 cm pour 10 m.s
-1
Le vecteur ∆
∆∆
∆ v (t
5
) est égale à la somme des deux vecteurs v (t
6
) et - v (t
4
).
v(t
6
) = 25 m.s
-1
et v(t
4
) = 15 m.s
-1
∆
∆∆
∆ v (t
5
) ∑  F
ext
=  P +  f
P
v (t
6
) - v (t
4
)  f
G
5
G
5
a
La somme vectorielle des deux forces agissant sur
le boulet est non nulle.
∑  F
ext
possède la même direction et le même sens
que ∆
∆∆
∆ v (t
5
) : la deuxième loi de Newton est vérifiée.

8.
a) Tracer sur le papier millimétré ci-dessous la représentation graphique v = f(t).
b) Déterminer l’équation de la courbe obtenue en expliquant ta démarche.
Equation de la courbe v = f(t) :
Il s’agit dune droite passant par l’origine traduisant une proportionnalité entre la vitesse instantanée v et le
temps t.
On peut alors écrire : v(t) = a.t avec a : coefficient directeur de la droite.
Déterminons la valeur de a :
a = v
2
– v
1
t
2
– t
1
= 25 – 5
2,5 – 0,5 = 10
Equation : v(t) = 10 x t
Remarque : L’unité de a est m.s
-1
/s soit m.s
-2
.
c) En déduire la vitesse du boulet à l’instant t
7
.
D’après la représentation graphique, on peut lire pour t
7
= 3 s v(t
7
) = 30 m.s
-1
On peut aussi utiliser l’équation de la droite pour calculer v(t
7
) :
v(t
7
) = 10 x 3 = 30 m.s
-1
+
+
+
+
+
+
v (m.s
-
1
)
t
(s)
20
10
2,0
1,0

9. Lorsque la hauteur de chute est beaucoup plus importante, l’allure de la courbe
v = f(t) est donnée par la courbe ci-contre :
a) La vitesse du boulet augmente-t-elle indéfiniment comme
le laissait penser la courbe obtenue à la question 8 ?
D’après la courbe v = (t) ci-contre on peut constater que la valeur de la
vitesse tend vers une valeur constante lorsque la hauteur de chute est
plus importante : la courbe présente un palier de vitesse.
b) Quelle est la particularité de la somme vectorielle
des forces appliquées au boulet lorsque la vitesse
atteint un palier ?
Lorsque la vitesse devient constante, et en vertu de la première loi de Newton (Principe d’inertie), on peut
affirmer que la somme vectorielle des deux forces appliquées au boulet est égale au vecteur nul :
∑  F
ext
=  P +  f =  0
00
0 ⇒
⇒⇒
⇒ P = -  f
Les deux forces se compensent, le poids P devient égal à la résistance de l’air f, et la vitesse v constante.