6a-Controle

J. ASTOLFI TS3
22 janvier 2015
CONTRÔLE de PHYSIQUE n°6
(Durée : 40 mn – Calculatrices autorisées)
 EXERCICE UNIQUE :
L’entraîneur obtient 3 graphes ci-dessous :
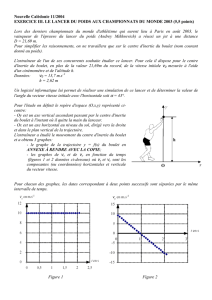
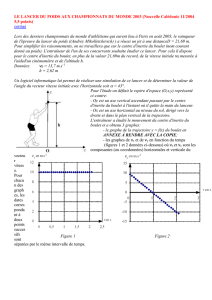
- Figures 1 et 2 : graphes représentatifs des fonctions Vx = f(t) et Vy = f(t) où Vx et Vy sont les
coordonnées du vecteur vitesse du boulet.
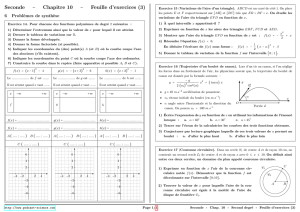
- Figure 3 : trajectoire du centre d’inertie G du boulet.
Lors des championnats du monde d'athlétisme qui eurent lieu à Paris en
août 2003, le vainqueur de l'épreuve du lancer du poids, le bélarusse
Andrey Mikhnevich, a réussi un jet à une distance D = 21,69 m.
L'entraîneur de l'un de ses concurrents souhaite étudier ce lancer en
travaillant sur le mouvement du centre d’inertie G du boulet. Pour cela, il
dispose de la valeur V0 du vecteur vitesse initiale de G et de l’altitude H du
même point à la date t = 0 : V0 = 13,7 m.s-1 et H = 2,62 m
Un logiciel informatique lui permet de réaliser une simulation de ce lancer
et de déterminer la valeur de l'angle  du vecteur vitesse initiale avec
l'horizontale :  = 43,0°.
L’étude est réalisée dans le repère (O, i, j ) représenté sur le schéma ci-
contre.
Figure 1
Figure 2
Figure 3

 Étude des conditions initiales du lancer
1. Déterminer graphiquement les composantes V0x et V0y du vecteur vitesse à l'instant t = 0 s.
2. En déduire que la valeur V0 du vecteur vitesse initiale du boulet et l'angle de tir  sont compatibles
avec celles données dans le texte.
3. Si l’on décompose le mouvement du boulet suivant les directions (Ox) et (Oy), que peut on dire de son
mouvement suivant ces 2 directions dans l’intervalle de temps [0 s ; 2,5 s] ? Justifier.
4. Déterminer graphiquement la durée mise par le boulet pour atteindre la sommet de sa trajectoire. On
justifiera brièvement.
 Étude théorique du mouvement du boulet
Donnée : champ de pesanteur terrestre : g = 9,81 m.s -2
On suppose que, compte tenu des faibles vitesses atteintes par le boulet, les frottements dus à l'air au cours
du jet sont négligeables.
5. En appliquant la 2ème loi de Newton dans le référentiel terrestre supposé galiléen, déterminer les
coordonnées du vecteur accélération du centre d'inertie du boulet lors du mouvement.
6. Établir les équations horaires du mouvement du centre d’inertie du boulet.
On détermine l’équation de la trajectoire en combinant entre elles les équations horaires et en « éliminant » le
paramètre temps. L’équation de la trajectoire obtenue est de la forme :
.
.
2
2
0
g
y(x) = x + (tanα).x
2(v cosα)
+ H
7. Calculer la portée théorique D’ du lancer. Les valeurs de D (figure 3) et D’ sont-elles en cohérence ?