Mouvement d`une particule dans un champ B

1 BC 7) M OUVEMENT D ' UNE C HARGE DANS UN C HAMP M AGNETIQUE 36
7) M OUVEMENT D ’ UNE C HARGE DANS UN C HAMP M AGNETIQUE
UNIFORME
1) Etude expérimentale et interprétation : manuel p.132
2) Force de Lorentz
a) Définition
Une charge q qui se déplace avec une vitesse
v
G
dans un champ magnétique caractérisé par le
vecteur
B
G
subit une force magnétique appelée force de Lorentz f
G
m
donnée par :
Bvqf
m
G
G
G
∧
=
m
f
G
est le produit vectoriel de qv
G
par B
G
.
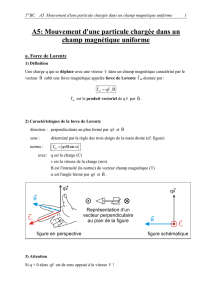
b) Caractéristiques de la force de Lorentz
direction : perpendiculaire au plan formé par vq
G
et B
G
sens : déterminé par la règle des trois doigts de la main droite (cf. figure)
norme : α= sinqvBf
m
avec: q est la charge (C)
v est la vitesse de la charge (m/s)
B est l'intensité (la norme) du vecteur champ magnétique (T)
α est l'angle formé par vq
G
et B
G
.
figure en perspective
Représentation d'un
vecteur perpendiculaire
au plan de la figure
figure schématique
qv qv
B
B
fm
fm
c) Application 1 manuel p.133

1 BC 7) MOUVEMENT D'UNE CHARGE DANS UN CHAMP MAGNETIQUE 37
3) Etude cinématique dans le cas où la vitesse initiale est perpendiculaire au
champ magnétique
Données : A l'instant initial une particule de masse m et de charge électrique q pénètre avec la
vitesse dans une région de l'espace où règne un champ magnétique uniforme G
B. On
suppose que est perpendiculaire à
0
v
G
G
0
v
G
B.
(t=0)
(t>0)
v
0
v
k
T
N
a
a
f
f
particule de
charge q>0 et
de masse m
C
orientation
de la trajectoire
B
O
M
champ magnétique
r
Nous étudions le mouvement de la particule à l'intérieur du champ uniquement.
a) Système. Référentiel. Repère
Le système est la particule chargée.
Le référentiel est celui du dispositif qui crée le champ magnétique (par exemple deux bobines
de Helmholtz).
Le repère est celui de Frenet (M, T
G
, N
K
,
k
G
).
k
G
est un vecteur unitaire perpendiculaire au plan
formé par T
G
et N
K
.
b) conditions initiales
t = 0 ⇒ particule en O (origine de la trajectoire curviligne)
vitesse = v
0
c) Forces extérieures
Force de Lorentz : Bvqf
m
G
G
G
∧
=
G
Le poids P est négligeable devant
G
f
m
. Il n’y a pas de frottement car le mouvement se fait dans
le vide.

1 BC 7) MOUVEMENT D'UNE CHARGE DANS UN CHAMP MAGNETIQUE 38
d) Accélération
Appliquons le principe fondamental de Newton (Newton II) :
amBvq
amF
G
G
G
G
G
=
=
∧
∑
Bv
m
q
a
G
G
G
∧
=
Projections sur les directions de
T
G
, N
K
et
k
G
:
0a
T
= (1)
m
vBq
a
N
= (2)
0a
k
= (3)
e) Vitesse et position
* (1) ⇒ v = constant
Conclusion : Le mouvement est uniforme.
* Comme la coordonnée normale de l'accélération s'écrit toujours
r
v
a
2
N
= (r = rayon du
cercle tangent), on a grâce à (2) :
Bq
mv
r
m
vBq
r
v
2
=
=
Comme m, v, q et B sont constants, r est constant !
Conclusion : Le mouvement est circulaire.
* (3) ⇒ v
k
= constant
Condition initiale: t = 0 ⇒ v
0k
= 0
Donc : v
k
= 0 pour tout instant t ⇔ il n'y a pas de mouvement suivant
k
G
!
Conclusion :
Le mouvement s'effectue dans un plan perpendiculaire à
G
B, contenant la vitesse initiale
G
v
o
f) Conclusion générale : nature du mouvement
Une particule chargée entrant dans un champ magnétique avec une vitesse perpendiculaire au
champ décrit un mouvement circulaire et uniforme dans un plan perpendiculaire au champ.
Le rayon de la trajectoire est donné par l'expression : Bq
mv
r= (4)

1 BC 7) MOUVEMENT D'UNE CHARGE DANS UN CHAMP MAGNETIQUE 39
g) Vitesse linéaire, vitesse angulaire, période, fréquence
La vitesse linéaire de la particule se déduit de (4) :
m
Brq
v=
La vitesse angulaire est reliée à la vitesse linéaire par
r
v
=ω
⇒
m
Bq
=ω
La période est reliée à la vitesse angulaire par
ω
π
=2 T ⇒ Bq
m
2T π=
La fréquence est reliée à la période par
T
1
f=
⇒
m
Bq
2
1
fπ =
Les expressions montrent que ω, T et f sont indépendants du rayon r et de la vitesse v.
h) Remarques
1) La force de Lorentz
G
f
m
est centripète. C'est elle qui est à l'origine du mouvement
circulaire et uniforme !
2) Si est parallèle à
0
v
G
B
G
la force de Lorentz est nulle et la particule décrit un
mouvement rectiligne et uniforme à travers le champ (Newton I).
3) Si l'angle entre
0
v
G
et B
G
est différent de 0° et de 90°, la particule décrit un mouvement
uniforme hélicoïdal (trajectoire = hélice).
i) Application 2 manuel p.136

1 BC 7) MOUVEMENT D'UNE CHARGE DANS UN CHAMP MAGNETIQUE 40
4) Déflexion magnétique. Tube de télévision : manuel p.137 et 138
Un faisceau de particules identiques (électrons), de charge q, de masse m, de vitesse ,
pénètre en un point O dans une région de l'espace de longueur
A , où règne un champ
magnétique
G
B, uniforme et perpendiculaire à
0
v
G
0
v
G
.
Dans le champ magnétique, les particules décrivent un arc de cercle de rayon R = CO = CS,
avec une valeur de vitesse constante v
0
. A leur sortie S de l’espace magnétique, les particules
ne sont soumises à aucune force et retrouvent une trajectoire rectiligne tangente à la trajectoire
circulaire dans le champ. Elles arrivent finalement en P sur un écran plan situé à la distance D
du point O. Leur interaction avec la couche fluorescente de l'écran y provoque la formation
d'un spot lumineux.
C
O
S
A
R
R
écran
fluorescent
P
O' O"
q<0
d
D
v
0
α
α
B
champ
magnétique
Soit O" le point d’impact des électrons sur l’écran en absence de champ magnétique. On se
propose de déterminer la déviation d = O"P subie par les électrons.
On suppose que
* la longueur
A de la région où règne le champ magnétique soit faible par rapport au
rayon R de la trajectoire ⇔ α est petit ⇔ tan α ≈ sin α ≈ α (5)
(α est exprimé en radians !);
*
A est faible par rapport à la distance D ⇔ O’O" ≈ D.
Alors :
D
d
"O'Od
tan ≈=α
(6)
R
sin A =α avec
eB
mv
R
0
= ⇒
0
mv
eB
sin A =α (7)
(5), (6) et (7) ⇒
0
mv
eB
D
dA
= ⇔ BD
mv
e
d
0
⋅⋅= A