APPROXIMATION DES SYST`EMES DE LOIS DE

APPROXIMATION DES SYST` EMES DE LOIS DE
CONSERVATIONS HYPERBOLIQUES
1. G´ en´ eralit´ es
1.1. ´ Equation de transport, courbe caract´eristique. Le Syst`eme de Lois de
Conservation (SLC) le plus simple `a ´etudier est l’´equation de transport scalaire 1D
qui s’´ecrit
(1) ct+ucx= 0.
La vitesse uest une constante et l’inconnue est une fonction c(t, x) qui d´epend du
temps tet de l’espace x. On ajoute `a cette ´equation une condition initiale
c(0, x) = c0(x).
Pour r´esoudre, on utilise la m´ethode des caract´eristiques. Une caract´eristique est
une courbe (t, x(t)) le long de laquelle la solution de (1) est constante. On a donc
d
dtc(t, x(t)) = 0,
ct+x0(t)cx= 0.
Ceci nous dit que x0(t) = u. La caract´eristique a donc pour param´etrage (t, x0+ut).
Il s’ensuit que
(2) c(t, x) = c0(x−ut).
Si on s’int´eresse `a la solution de (1) dans un intervalle ]0, L[, on constate alors que
l’on ne peut pas imposer des CL des deux cˆot´es (si u > 0, il faut imposer c(t, 0) = cg
et si u < 0, il faut imposer c(t, L) = cd.)
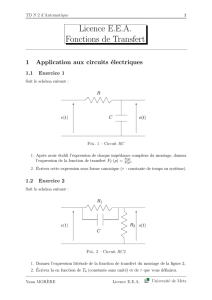
Exercice 1. R´esoudre, pour une vitesse donn´ee u > 0, le probl`eme
ct+ucx= 0, t > 0, x ∈]0, L[,
c(0, x) = c0(x), x ∈]0, L[,
c(t, 0) = g(t).
1.2. Syst`eme de Friedrichs. On peut alors s’int´eresser au cas du syst`eme lin´eaire
1D du premier ordre (o`u syst`eme de Friedrichs). Le probl`eme se pose
ct+Acx= 0, t > 0, x ∈R,(3)
c(0, x) = c0(x).(4)
O`u Aest une matrice m×m, le vecteur c(t, x) de taille mest l’inconnue.
Si la matrice Adu syst`eme de Friedrichs (3) est diagonalisable avec des valeurs
propres r´eelles, le syst`eme est dit (strictement) hyperbolique.
On notera (rk)k=1···mles mvecteurs propres (`a droite) de cette matrice et
(λk)k=1···mles valeurs propres correspondantes.
Exercice 2. Montrer que le probl`eme (3), (4) admet une solution et une seule dans
C0([0, T ], L2(R)) quand la condition initiale c0est dans L2. Utiliser une transform´ee
de Fourier. Que se passe-t-il si Aest r´eelle mais pas ses valeurs propres ?
Exercice 3. Calculer la solution du probl`eme (3), (4) dans le cas o`u la condition
initiale s’´ecrit
c0(x) = cgsi x < 0,
cdsi x > 0.
1

2 APPROXIMATION DES SYST` EMES DE LOIS DE CONSERVATIONS HYPERBOLIQUES
Trouver une formule simple pour Ac(t, 0), utilisant les notations v+= max(v, 0), et
v−= min(v, 0).
1.3. ´ Equation de Burgers. Les choses se compliquent quand les ´equations devi-
ennent non-lin´eaires. L’exemple le plus simple pour voir se qui se passe est donn´e
par l’´equation de Burgers
ut+u2
2x
= 0,(5)
u(0, x) = u0(x).(6)
Exercice 4. Montrer que mˆeme si la condition initiale est r´eguli`ere, il n’existe pas
toujours de solution r´eguli`ere. Pour cela, consid´erer une condition initiale de classe
C∞qui v´erifie u(x) = 1 si x < 0 et u(x) = 0 si x > 1. Utiliser la m´ethode des
caract´eristiques.
Cet exercice montre qu’il est n´ecessaire d’´etendre la notion de solution (ici forte).
Pour cela, il est tentant de multiplier l’´equation (5) par une fonction test et d’int´egrer
par parties. On choisit la fonction test ϕdans C∞
0(R+×R).Attention cet espace est
diff´erent de C∞
0(R+∗×R), car la fonction test a le droit d’ˆetre non nulle en t= 0,
ce qui nous permettra d’imposer de mani`ere faible la condition initiale. Il vient
Zt≥0Zx∈R
ϕut+ϕu2
2x
= 0,(7)
Zt≥0Zx∈R−ϕtu−ϕxu2
2−Zx∈R
ϕ(t, ·)u0= 0.(8)
L’int´erˆet de cette derni`ere ´ecriture est qu’il n’y a plus de d´eriv´ee sur uet qu’elle a
donc encore un sens quand uappartient (par exemple) `a C([0, T ], L∞).D’o`u la
D´efinition 1. La fonction ude C([0, T ], L∞) est une solution faible du probl`eme
(5), (6) ssi la relation (8) est vraie pour toute fonction test ϕde C∞
0(R+×R).
Exercice 5. Le calcul pr´ec´edent montre que si u∈C1([0, T ]×R) est une solution
forte de (5), (6) alors uest forc´ement une solution faible. Montrer que la r´eciproque
est vraie.
Si une solution faible pr´esente une discontinuit´e, nous allons voir que nous pou-
vons tirer de la d´efinition 1 une relation appel´ee relation de saut ou de Rankine-
Hugoniot. On suppose donc que uest de classe C1sauf sur une ligne de discontinuit´e
param´etr´ee par (t, x(t)). On note σ=x0(t) la vitesse de la discontinuit´e. On note
uget udles valeurs de ude part et d’autre de la discontinuit´e et [u] = ud−ugle
saut de u`a travers la discontinuit´e.
Proposition 1. Si uest solution faible de l’´equation de Burgers, alors usatisfait
la relation de saut u2
2=σ[u],
soit encore
(9) ug+ud
2=σ.
Cette relation de saut peut se g´en´eraliser pour les solutions faibles d’une ´equation
du type G(u)t+F(u)x= 0. La relation de saut est alors σ[G(u)] = [F(u)]. Attention,
certains calculs formels ne sont plus valables avec les solutions faibles comme le
montre l’exercice suivant.
Exercice 6. V´erifier qu’une solution faible de ut+ (u2/2)x= 0 n’est pas forc´ement
solution faible de (u2/2)t+ (u3/3)x= 0. Pour cela, consid´erer la fonction
u(t, x) = 1 si x < 0,
0 si x > 0.

APPROXIMATION DES SYST` EMES DE LOIS DE CONSERVATIONS HYPERBOLIQUES 3
La proposition 1 va nous permettre de v´erifier que, malheureusement, il peut
y avoir plusieurs solutions faibles `a l’´equation de Burgers. L’espace de d´epart de
recherche de la solution forte a ´et´e trop “agrandi”.
Exercice 7. On pose
u0(x) = 0 si x < 0,
1 si x > 0.
Soient alors les deux fonctions u1(t, x) et u2(t, x) d´efinies par
u1(t, x) = 0 si x/t < 1/2,
1 si x/t > 1/2.
et
u2(t, x) = 
0 si x/t < 0,
x/t si 0 < x/t < 1,
1 si x/t > 1.
Montrer qu’elles sont toutes les deux solutions de (5), (6).
En raisonnant sur les caract´eristiques, Lax a propos´e une condition assez simple
pour ´eliminer les solutions suppl´ementaires. Pour que le probl`eme d’´evolution soit
bien pos´e en pr´esence d’un choc (c’est un autre nom pour “discontinuit´e”) , il faut
pouvoir d´eterminer les propri´et´es du choc : sa vitesse σet les valeurs de uget udsur
le choc, soit trois inconnues. La relation de saut de Rankine-Hugoniot (9) fournit une
´equation. Si la courbe caract´eristique venant de la gauche va plus vite que le choc,
i.e. ug> σ et si le choc rattrape la caract´eristique venant de la droite i.e. σ > ud,
alors, on dispose de deux ´equations suppl´ementaires. Mais comme σ= 1/2(ug+ud)
est compris entre uget ud, la condition de Lax s’´ecrit
(10) ug> ud.
D´efinition 2. Une solution de Lax est une solution faible qui v´erifie en plus (10)
sur les chocs.
On admet que cette solution est cette fois unique.
Exercice 8. Calculer la solution de Lax du probl`eme
ut+ (u2/2)x= 0,
u(0, x) = 
1 si x < 0,
1−xsi 0 <x<1,
0 si 1 < x.
Exercice 9. Calculer la solution de Lax du probl`eme (dit probl`eme de Riemann)
ut+ (u2/2)x= 0,
u(0, x) = ugsi x < 0,
udsi x > 0.
Calculer, en particulier, u(t, 0+)2/2 et u(t, 0−)2/2. V´erifier que ces deux quantit´es
sont ´egales. Retrouver ce r´esultat `a partir de la condition de saut.
1.4. Sch´ema de Godunov. Le sch´ema de Godunov est un sch´ema tr`es simple
pour approcher la solution de Lax de (5), (6). On se donne un pas de temps τ, un
pas d’espace h. La discr´etisation est d´efinie par xi=ih et tn=nτ. Les cellules sont
des intervalles centr´es sur les points de discr´etisation
Ci=]xi−1/2, xi+1/2[.
L’approximation un
iest d´efinie par
un
i'u(tn, xi).

4 APPROXIMATION DES SYST` EMES DE LOIS DE CONSERVATIONS HYPERBOLIQUES
Pour initialiser l’algorithme, u0
ipeut ˆetre d´efini par exemple par la valeur moyenne
sur la cellule Cide la condition initiale
u0
i=1
hZxi+1/2
xi−1/2
u(0, x)dx.
Le sch´ema de Godunov est bas´e sur la r´esolution exacte du probl`eme de Riemann
(introduit `a l’exercice 9)
vt+ (v2/2)x= 0,
v(0, x) = vgsi x < 0,
vdsi x > 0.
La solution de ce probl`eme ne d´epend que du rapport x/t (elle est dite auto-
similaire.) La solution de ce probl`eme peut donc ˆetre not´ee
v(t, x) = R(x/t, vg, vd).
Pour passer de l’instant n`a l’instant n+ 1, l’id´ee est de r´esoudre exactement le
probl`eme d’´evolution suivant pendant un pas de temps τ
vt+ (v2/2)x= 0,
v(0, x) = un
ipour x∈Ci.
Si le pas de temps est assez petit, il suffit pour cela de r´esoudre un probl`eme de
Riemann pour chaque point xi+1/2(aux interfaces des cellules Ci.) Les solutions
des probl`emes de Riemann n’interagissent pas entre elles sous la condition de type
CFL
τ < h
supi|un
i|.
La solution `a l’´etape n+ 1 est alors la moyenne sur chaque cellule de la solution v
`a l’instant τ.
un+1
i=1
hZxi+1/2
xi−1/2
v(τ, x)dx.
Exercice 10. En int´egrant la loi de conservation (5) sur ]tn, tn+1[×Ci, montrer que
le sch´ema de Godunov peut s’´ecrire
un+1
i−un
i
τ+Fn
i+1/2−Fn i−1/2
h= 0,
avec
Fn
i+1/2=R(0+ ou −, un
i, un i−1)2/2.
Exercice 11. Programmer le sch´ema de Godunov et v´erifier num´eriquement qu’il
converge dans le cas de la solution de l’exercice 8.
2. Le probl` eme de Riemann
R´esoudre le probl`eme de Riemann, c’est trouver la solution de Lax de
wt+f(w)x= 0,(11)
w(0, x) = wgsi x < 0,
wdsi x > 0.
(12)
Ici, le syst`eme de lois de conservation consid´er´e est de taille m. Le vecteur des
variables conserv´ees west donc dans Rmet le flux fest une application, en g´en´eral
non-lin´eaire, de Rmdans Rm. On note A(w) la jacobienne du flux
A(w) = f0(w) = 
∂f1
∂w1··· ∂f1 ∂wm
.
.
.....
.
.
∂fm
∂w1··· ∂fm ∂wm
.

APPROXIMATION DES SYST` EMES DE LOIS DE CONSERVATIONS HYPERBOLIQUES 5
Le syst`eme est suppos´e hyperbolique. La jacobienne A(w) est donc diagonalisable
avec des valeurs propres r´eelles. Les valeurs propres sont not´ees λi(w) et les vecteurs
propres correspondants sont ri(w) pour 1 ≤i≤m. Dans un premier temps, nous
supposerons que les champs sont tous vraiment non lin´eaires, c’est `a dire que pour
tout i, et pour tout ´etat w,
(13) ∇λi(w)·ri(w)6= 0.
Nous supposons aussi que les valeurs propres peuvent ˆetre ordonn´ees
λ1(w)< λ2(w)<··· < λm(w).
Dans cette section, nous introduisons les notions n´ecessaires `a la r´esolution du
probl`eme de Riemann (11), (12) : ondes simples, invariants de Riemann, chocs. Nous
illustrerons ces notions sur l’exemple des ´equations de Saint Venant pour mod´eliser
les ´ecoulements en eau peu profonde.
2.1. ´ Equations de Saint Venant. Les ´equations de Saint-Venant s’´ecrivent :
ht+ (hu)x= 0,
(hu)t+ (hu2+gh2
2)x+ghax= 0.
Les inconnues sont la hauteur d’eau h(t, x) et la vitesse horizontale u(t, x) de
la colonne d’eau. a(x) est la hauteur du fond. La surface libre se trouve donc `a la
hauteur h+a.
Dans le cas de solutions r´eguli`eres, les ´equations de Saint-Venant impliquent la
conservation de l’´energie
E=hu2
2+gh2 2+gha,
qui s’´ecrit
Et+ ((E+gh2
2)u)x= 0.
Dans le cas de solutions discontinues la derni`ere ´egalit´e devient une in´egalit´e.
Et+ ((E+gh2
2)u)x≤0.
Supposons que le fond est plat, i.e. que ax= 0. En posant
(14) w=w1
w2=h hu ,
et
(15) f(w) = hu
hu2+gh2
2="w2
w2
2
w1+g 2w2
1#.
Les ´equations de Saint Venant prennent la forme d’un syst`eme non-lin´eaire du pre-
mier ordre
wt+f(w)x= 0.
Exercice 12. V´erifier que ce syst`eme est hyperbolique, calculer les vecteurs propres
et les valeurs propres. V´erifier que tous les champs sont vraiment non-lin´eaires.