UMBB STH Faculté des sciences 2011/2012 Département de

UMBB STH
Faculté des sciences 2011/2012
Département de Physique
Physique2
ETLD 2
Exercice 1 : (05 points)
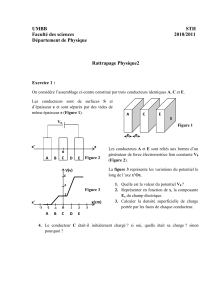
Trois charges ponctuelles
12 3
2 et qq q q C
sont placées comme l’indique la figure 1.
1. Calculer
3
q
pour que le vecteur champ électrique au point M soit nul.
2. Calculer le potentiel électrique résultant au point M.
3. Calculer l’énergie interne du système.
On donne :
10 a cm
Exercice 2 : (10 points)
Une sphère de centre O, de rayon R est chargée en volume avec une densité non uniforme
( ) 0r
.
Le champ électrique crée par cette répartition de charge est défini par :
0
2
2
0
( ) pour 0
2
1
( ) pour
2r
k
E r r R
kR
E r r R
1. Déterminer le potentiel électrique V(r) de cette distribution de charge. On prendra
l’infini comme origine des potentiels
V(r )=0
.
2. Tracer la courbe de V(r).
3. Déterminer la densité de charge volumique
()r
de cette distribution de charge.
4. Déterminer la charge totale
T
Q
de cette répartition de charge.
5. Tracer la courbe de
()r
.
Exercice 3 : (05 points)
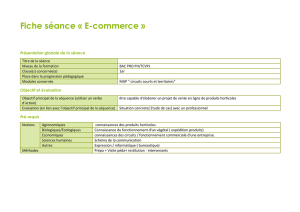
Soit le circuit électrique de la figure 2.
On donne : E1=12V, E2=6V, e=3V
R1=5Ω, R2=4Ω,
r1= 1Ω, r2=2Ω, r=2Ω.
1. Calculer l’intensité des courants qui circulent dans chaque branche et préciser leurs
sens.
2. Déterminer l’énergie dissipée par effet joule dans ce circuit pendant 6 minutes de
fonctionnement.
3. Calculer le rendement du générateur E1 et du récepteur e.
2a
q1
q2
q3
Y
X
O
2a
a
a
M
R1
R2
r1
r
E1
e
C
D
r2
E2
A
F
E
B
Figure 1
Figure 2

UMBB STH
Faculté des sciences 2011/2012
Département de Physique
Corrigé Physique2
ETLD 2
Exercice 1: (5 points)
1. Calcul de
3
q
pour que le vecteur champ électrique au point M soit nul.
2. Calcul du potentiel électrique résultant au point M.
3. Calcul de l’énergie interne du système.
Exercice 2 : (10 points)
1. Le potentiel électrique V(r) de la distribution de charge
()r
.
( ) ( )E gradV V r E r dr C
Pour
0rR
:
1 1 1 1
0
11
0
( ) ( ) 2
() 2
k
V r E r dr C dr C
k
V r r C
0.5
0.5
0.5
0.5
0.5
0.25
Figure 1
2a
q1
q2
q3
Y
X
O
2a
a
a
M
0.25
0.25
0.25
0.5
0.5
0.5
0.5
0.5

UMBB STH
Faculté des sciences 2011/2012
Département de Physique
Pour
rR
:
2
2 2 2 2
2
0
2
22
0
1
( ) ( )
2r
1
( )
2r
kR
V r E r dr C dr C
kR
V r C
Avec :
2
2 2 2 0
1 2 1 1
00
1
( ) 0 0 ( )
2r
( ) ( ) ( ) ( 2 )
2
rkR
V r C V r
kR k
V R V R C V r r R
2. Tracé de la courbe de V(r).
3. La densité de charge volumique
()r
:
Suivant le théorème de Gauss :
int
0
.er
Q
E dS
2
int
0 0 0
2
0
( ) ( )4
( )4 ......................( )
er
dQ r dV r r dr
d
d r r A
dr
2
2
. ( ) ( )4
4 ( ( ) )...................( )
E dS E r dS E r r
dd
E r r B
dr dr
2
0
2
(A)=(B) ( ) ( ( ) )
d
r E r r
r dr
Pour
0rR
:
2
0
20
( ) ( ) ( )
2
d k k
r r r
r dr r
Pour
rR
:
22
0
22
0
1
( ) ( ) ( ) 0
2r
d kR
r r r
r dr
R
r
V(r)
0.5
0.5
0.5
0.5
0.5
0.5
01
0.5
01
0
kR
0
2
kR
0.5
01

UMBB STH
Faculté des sciences 2011/2012
Département de Physique
4. La charge totale
T
Q
:
2
0
22
0
( ) ( )4
( )4 2
R
TV
R
T
Q r dV r r dr
k
Q r dr k R
r
5. Tracé de la courbe de
()r
.
Exercice 3 : (05 points)
1. Calcul de l’intensité des courants qui circulent dans chaque branche.
1 2 3
1 1 1 2 2 2 3 1 2
1 2 2 2 3 2
0 Noeud C
( ) ( ) 0
0 ( )
i i i
r R i r R i i E E Maille ACDBA
i r R i ri E e Maille CEFDC
11
22
33
1,1 dirigé de Avers C
0,1 dirigé de D vers C
1,2 dirigé de C vers E
i A i
i A i
i A i
2. L’énergie dissipée par effet joule dans le circuit pendant 6 minutes de fonctionnement.
2 2 2
J 1 1 1 2 2 2 3
J
W = ( ) ( )
W (10,2)6.60 3,67
r R i r R i ri t
KJ
3. Le rendement du générateur E1 et du récepteur e.
1
1 1 1
13
91% , 56 %
Ee
E ri e
E e ri
r
R
k
R
()r
0.5
0.5
0.5
0.5
0. 25
0.25
0.75
0.75
0.75
1
0.5
0.5
0.25
01
0.25