Amphi 1 (diapos avec corrections des quiz)

www.orolia.com
Frédéric Chevy, Jérôme Faure, Karyn Le Hur, Luca Perfetti,
Pascale Senellart, Jean-Eric Wegrowe, Manuel Joffre
Poursuite de l’apprentissage des principes fondamentaux (Pauli)
Nouvelles méthodes pour traiter des problèmes plus complexes (3D)
Exploitation des symétries du système (translation, rotation, …)
Méthodes d’approximation (perturbations, variations, …)
Structure de la matière : atomes, molécules, solides
Quelques exemples de technologies quantiques (horloges atomiques,
spectroscopie infrarouge, détecteurs à puits quantiques, etc.)
Physique quantique avancée

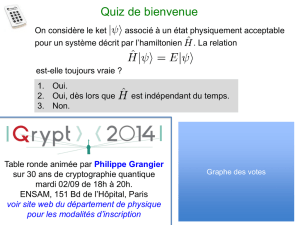
1. Oui.
2. Oui, dès lors que est indépendant du temps.
3. Non.
est-elle toujours vraie ?
On considère le ket associé à un état physiquement acceptable
pour un système décrit par l’hamiltonien . La relation
Quiz de bienvenue
TexPoint fonts used in EMF.
Read the TexPoint manual before you delete this box.: AAAAAA

- Diapos et simulations présentées en amphi
- Guide de lecture du livre (correspondance amphis – chapitres)
- Questionnaires en ligne (chaque semaine avant lundi 9h00)
- Boîtiers de vote électronique
https://moodle.polytechnique.fr/course/view.php?id=1890
Jean-Louis Basdevant
&
Jean Dalibard
Ressources pédagogiques
Participation au QCM contribue à la note de PC
(avec Devoirs à la Maison et participation en PC)
Chapitres 1 à 17
(sauf 15.1-15.3)

 Etat quantique d’un système
 Mesure
 Evolution temporelle
 Commutation des observables
Amphi 1 :
Les principes de la physique quantique
Chapitres 5 et 7

1.
Etat quantique d’un système