Feuille d`exercices

EXERCICES ET PROBLÈMES
Ch. 14 : Angles inscrits, angles au centre
: Oral : Application : Approfondissement
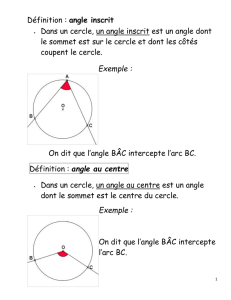
Vocabulaire
1Les points , , et sont sur le cercle
de centre .
1. Citer deux angles au centre du cercle en
précisant l’arc de cercle qu’ils interceptent.
2. Citer deux angles inscrits du cercle qui
interceptent l’arc .
3. Citer, dans le cercle , un angle inscrit et
l’angle au centre qui interceptent l’arc .
2La figure ci-dessous représente un cercle
de centre .
Pour chaque angle inscrit cité ci-après, indiquer
l’angle au centre qui intercepte le même arc et pré-
ciser le nom de l’arc.
1.
2.
3.
4.
5. d
6. d
3Le point est le centre du cercle passant
par les points , , , et .
En s’aidant éventuellement d’une figure à main le-
vée :
1. Citer des angles inscrits qui interceptent l’arc
.
2. Citer l’angle au centre qui interceptent l’arc
.
3. Citer l’angle au centre et un angle inscrit qui
interceptent le même arc .
Propriétés
4Dans un cercle, un angle inscrit et un angle
au centre interceptent le même arc.
1. Quelle est la mesure de l’angle au centre
lorsque l’angle inscrit mesure :
(a) ˚?
(b) ˚?
(c) ˚?
(d) ˚?
2. Quelle est la mesure de l’angle inscrit lorsque
l’angle au centre mesure :
(a) ˚?
(b) ˚?
(c) ˚?
(d) ˚?
5Dans la figure ci-dessous, , et sont trois
points du cercle de centre tels que : d˚
et ˚.

Calculer la mesure des angles det d.
6Les points , et sont sur le cercle
de centre .
1. (a) Reproduire la figure à main levée, puis
colorer en rouge l’angle et l’arc
qu’il intercepte.
(b) Colorer en vert l’arc intercepté par
l’angle au centre .
2. Quelle est la mesure de l’angle ? Jus-
tifier.
7La figure ci-dessous représente un cercle de
centre .
Déterminer, en justifiant, la mesure de l’angle .
8Dans la figure ci-dessous, les points , et
appartiennent au cercle de centre tels que :
det d˚, strictement positif.
1. Calculer .
2. En déduire la nature du triangle .
9Sur la figure ci-dessous, les droites
et se coupent en , point d’intersection des
cercles et . Le point est le centre du
cercle .
Calculer la mesure de l’angle . Justifier votre
démarche.
10 Les points , , et sont sur le cercle
de centre .
est un diamètre de ce cercle.
1. (a) Quelle est la nature du triangle ?
(b) En déduire la mesure de l’angle .
2. Déterminer la mesure de l’angle .

3. (a) Quelle est la nature du triangle ?
(b) Déterminer la mesure de l’angle .
11 Les points , , et sont sur le cercle
.
1. Déterminer la nature exacte du triangle
.
2. Déterminer la mesure des angles et
puis celle de l’angle .
12 Sur la figure à main levée ci-dessous, les
droites et se coupent en .
1. Calculer la mesure de l’angle puis celle
de l’angle . Justifier votre démarche.
2. Le point est-il le centre du cercle ? Justi-
fier.
Problèmes
13 Deux droites parallèles coupent un cercle
de centre respectivement en et et en et
.
On appelle le point d’intersection des droites
et .
1. À l’aide de considérations sur les angles, dé-
montrer que le triangle est isocèle.
2. Démontrer que la droite est perpendi-
culaire à la droite .
14 Soit un triangle et son centre cir-
conscrit. On appelle le point d’intersection de la
hauteur issue de et de , et le point d’in-
tersection de la hauteur issue de et de . Soit
l’orthocentre du triangle . La droite
recoupe le cercle en .
1. Tracer une figure, éventuellement avec un
logiciel de géométrie dynamique (si le tra-
vail est fait à la maison).
2. Que pouvez-vous dire des angles et
d?
3. En comparant les angles des triangles
et , démontrer que d.
4. En déduire que est le symétrique de par
rapport à la droite .
5. En procédant de la même façon, que peut-on
démontrer concernant les trois symétriques
de l’orthocentre par rapport à chacun des
côtés du triangle ?
15 Les points , , , et sont sur le cercle
de centre . On donne ˚ et ˚.
1. Déterminer la mesure des angles et
.
2. Déterminer la mesure des angles det
d.