TD_1_a_9

1
TD Biomécanique et Analyse du Mouvement
M1-Sc2
TD N°1 : CINEMATIQUE
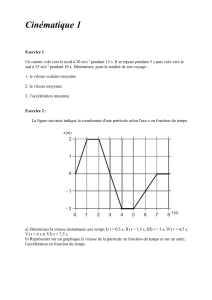
Exercice 1 : Déplacement, vitesse et accélération instantanées
Le tableau ci-dessous présente les enregistrements des positions d’un objet animé d’un
mouvement unidirectionnel en fonction du temps. A partir de ces données, tracez :
– La courbe du déplacement ;
– Les courbes de la vitesse et de l’accélération calculées par différences finies « pas à
pas » et différences finies « centrées ».
En sachant que l’équation mathématique qui décrit la courbe du déplacement (d) en
fonction du temps (t) est : d = 2 × cos(10 × t) + 0,5 × t 5 + 3 × t2 - 2 × t + 1, calculez à chaque
instant t la valeur exacte de la vitesse et de l’accélération.
Rappel : Dérivée de f ((g(x)) = g ' (x) * f ' (g(x)) et sin’(x)=cos(x) ; cos’(x)= - sin(x)
Comment pouvez vous expliquer les variations observées entre les différentes courbes
de vitesse et d’accélération ? Dans le domaine de l’analyse du mouvement, quelle méthode de
calcul pouvez vous suggérer pour calculer la vitesse et l’accélération avec la plus grande
précision ?
Temps (s)
Position (m)
Temps (s)
Position (m)
0,05
2,66
0,55
2,25
0,10
1,91
0,60
2,84
0,15
0,91
0,65
2,98
0,20
-0,11
0,70
2,66
0,25
-0,91
0,75
2,00
0,30
-1,31
0,80
1,19
0,35
-1,20
0,85
0,48
0,40
-0,62
0,90
0,10
0,45
0,29
0,95
0,20
0,50
1,33
1,00
0,82

2
Exercice 2 : Angles segmentaires et inter-segmentaires
La figure ci-dessous représente une gymnaste au dernier instant de la phase d’impulsion
d’un flip arrière. Chaque articulation corporelle est représentée par un marqueur dont les
coordonnées dans le repère {O, x, y} sont obtenues à l’aide d’un système d’analyse
cinématique vidéo.
A partir de ces informations, calculez chacun des angles θ1 et θ2 en utilisant d’une part
une méthode trigonométrique (arctangente) et d’autre part une méthode vectorielle (produit
scalaire).
0.3
0.6
0.9
1.2
1.5
1.8
0.3
0.6
x (m)
y (m)
O
θ1
θ2

TD Biomécanique et Analyse du Mouvement
M1-Sc2
TD N°2 : CINEMATIQUE
Exercice 1 – Cinématique : Modélisation balistique du shoot au basket
Lors d’un match de basket, pour marquer un panier, il faut que le ballon passe dans un
cercle métallique situé dans un plan horizontal à 3,05 m du sol. Pour simplifier, on remplacera
le ballon par un point matériel devant passer exactement au centre C du cercle métallique. On
suppose que la trajectoire démarre en B, à une altitude h0 au-dessus du sol, et que la vitesse de
lancement v0 fait un angle α avec le plan horizontal (α = 45 ; g = 10 m·s-2 ; h0 = 2 m).
– Etablir les équations horaires de cette trajectoire après le lancer et en déduire
l’équation du mouvement. Quelle est la nature de la trajectoire ?
– Le basketteur se situe à 7,10 m du panier. Quelle doit être la valeur de v0 pour que le
panier soit réussi ?
– Combien de temps met la balle pour effectuer ce trajet ?
– A quelle hauteur passe la balle à mi-parcours ?
– Voulant arrêter le ballon, un adversaire, situé à 0,90 m du tireur, saute verticalement
en levant les bras. La hauteur atteinte par ses mains est de 2,70 m par rapport au sol. Les
valeurs de α et v0 étant les mêmes que dans le cas précédant, le panier sera-t-il marqué ?
Exercice 2 – Cinématique : Modélisation balistique du passage de relais
Lors d’une course de relais on représente deux coureurs (C1 et C2) d’une même équipe
de la manière suivante :
– A t0 = 0 s on a :
Pour C1 : position = x10, vitesse = v1 = 10 m·s-1, accélération = 0 m·s-2
Pour C2 : position = 0 m, vitesse = 0 m·s-1, accélération = γ2 = 3 m·s-2
– Au moment de la transmission, on a : Distance entre C1 et C2 = 1 m
Vitesse C1 = Vitesse C2
A partir de l’ensemble de ces données :
– Déterminez les équations horaires de C1 et de C2 tions horaires de C1 et de C2
– Calculez l’instant t de la transmission – Calculez l’instant t de la transmission
– Quel est l’écart de distance qui sépare C1 et C2 à t0 : x10 – Quel est l’écart de distance qui sépare C1 et C2 à t0 : x10

Exercice 3 – Cinématique : Rebond d’une balle
Une balle est lancée verticalement vers le bas d’une hauteur h = 70 cm avec une vitesse
initiale V0. Après l’impact au sol elle remonte à la même hauteur h.
– Quelle est la vitesse de la balle (V2) à l’instant de la remontée ?
– Si le coefficient de restitution lié à la déformation de la balle lors de l’impact au sol
vaut k = 0,76, quelle est la vitesse de la balle (V1) lors du contact au sol ?
– Quelle vitesse (V0) doit être donnée à la balle pour qu’elle remonte à la hauteur h ?

TD Biomécanique et Analyse du Mouvement
M1-Sc2
TD N°2 : CINEMATIQUE
Exercice 1 – Cinématique : Modélisation balistique du shoot au basket
Lors d’un match de basket, pour marquer un panier, il faut que le ballon passe dans un
cercle métallique situé dans un plan horizontal à 3,05 m du sol. Pour simplifier, on remplacera
le ballon par un point matériel devant passer exactement au centre C du cercle métallique. On
suppose que la trajectoire démarre en B, à une altitude h0 au-dessus du sol, et que la vitesse de
lancement v0 fait un angle α avec le plan horizontal (α = 45 ; g = 10 m·s-2 ; h0 = 2 m).
– Etablir les équations horaires de cette trajectoire après le lancer et en déduire
l’équation du mouvement. Quelle est la nature de la trajectoire ?
– Le basketteur se situe à 7,10 m du panier. Quelle doit être la valeur de v0 pour que le
panier soit réussi ?
– Combien de temps met la balle pour effectuer ce trajet ?
– A quelle hauteur passe la balle à mi-parcours ?
– Voulant arrêter le ballon, un adversaire, situé à 0,90 m du tireur, saute verticalement
en levant les bras. La hauteur atteinte par ses mains est de 2,70 m par rapport au sol. Les
valeurs de α et v0 étant les mêmes que dans le cas précédant, le panier sera-t-il marqué ?
Exercice 2 – Cinématique : Modélisation balistique du passage de relais
Lors d’une course de relais on représente deux coureurs (C1 et C2) d’une même équipe
de la manière suivante :
– A t0 = 0 s on a :
Pour C1 : position = x10, vitesse = v1 = 10 m·s-1, accélération = 0 m·s-2
Pour C2 : position = 0 m, vitesse = 0 m·s-1, accélération = γ2 = 3 m·s-2
– Au moment de la transmission, on a : Distance entre C1 et C2 = 1 m
Vitesse C1 = Vitesse C2
A partir de l’ensemble de ces données :
– Déterminez les équations horaires de C1 et de C2
– Calculez l’instant t de la transmission
– Quel est l’écart de distance qui sépare C1 et C2 à t0 : x10