EXERCICE II Un service au tennis (5,5 points)

Exercice 2 : Etude d’un service au tennis.
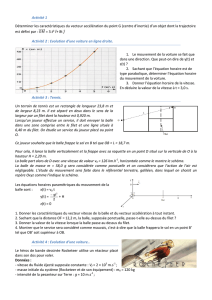
Un terrain de tennis est un rectangle de longueur 23,8 m et de largeur 8,23 m. Il est séparé en deux dans le sens de la largeur par
un filet dont la hauteur est 0,92 m.Lorsqu’un joueur effectue un service, il doit envoyer la balle dans une zone comprise entre le
filet et une ligne située à 6,40 m du filet pour que le service soit correct.
On se propose d’étudier le service d’un joueur placé au point O et qui souhaite envoyer la balle en B tel que : OB = L = 18,70m
Pour cela, il lance la balle verticalement et la frappe avec sa raquette en un point G0 situé sur la verticale de O à la hauteur H
=2,20 m. La balle part alors de G0 avec une vitesse de valeur v0 = 126 km.h-1, horizontale comme le montre le schéma ci-dessous.
La balle de masse m = 58,0 g sera considérée comme ponctuelle et on considérera que l’action de l’air est négligeable.
Question : Le service du joueur est il correct ?
Afin de vous guider dans votre démarche pour répondre à cette problématique vous suivrez les étapes suivantes :
 Etape 1 ANALYSER : Indiquez en quelques lignes la méthode que vous allez utiliser.
 Etape 2 REALISER : En suivant votre méthode décrite dans l’étape 1. Etablir avec rigueur les équations littérales
nécessaires pour répondre à la question.
 Etape 3 VALIDER : Faire les calculs numériques nécessaires pour valider ou non le service du joueur.
Votre étude du mouvement sera faite dans le référentiel terrestre, galiléen, dans lequel on choisit un repère Oxy comme l’indique
le schéma ci-dessous :
COMPETENCES
A
B
C
D
E
ANALYSER
REALISER
VALIDER
COMMUNIQUER
B
O
L
Filet
0
v
i
j
O
y
D
F
Filet
B
x
6,40 m
OF = 12,20 m.
OB = 18,70 m

Correction de l’exercice 2
Etape 1 Analyser : On utilise la méthode pour l’étude du mouvement d’un système dans un champ de pesanteur uniforme.
Après avoir défini le système (la balle de tennis que l’on considère comme ponctuelle) ,le référentiel (terrestre supposé galiléen) et
le bilan des forces pour notre système, on applique la deuxième loi de Newton.
On en déduit alors le vecteur accélération puis le vecteur vitesse et enfin le vecteur position. A partir des équations horaires on
établit l’équation de la trajectoire qui nous permettra d’effectuer de trouver les coordonnées du point de chute (la portée de la
balle).Il suffira de comparer avec les coordonnées du point B et de dire si le service est correct ou non.
Etape 2 Réaliser: La balle, dans le référentiel terrestre galiléen, est soumise uniquement à son poids
P
. En effet d’après l’énoncé
« l'action de l'air est négligeable » : on ne tient pas compte de la poussée d’Archimède et de la force de frottement de l’air sur la
balle. Et la raquette n’agit plus pendant le mouvement de la balle.
Les caractéristique du poids
P
= m.
g
sont :
- direction : verticale
- sens : vers le bas
- expression : P = m.g
-valeur (= grandeur) : P = 58,010-39,81 = 0,569 N.
La seconde loi de Newton, appliquée à la balle donne :
P
= m.
a
soit m.
g
= m.
a
d’où :
a
=
g
Les coordonnées du vecteur accélération dans le repère Oxy sont :
x
y
z
a0
a a g
a0
dv
ag
dt
donc
x
x
y
y
z
z
dv
a0
dt
dv
a a g
dt
dv
a0
dt
ainsi
x1
y2
z 13
vC
v(t) v g.t C
vC
C1, C2 sont des constantes définies par les conditions initiales.
Initialement
0
v(0) v
avec
0x 0
0 0y
0z
vv
v v 0
v0
donc
x 1 0
y2
z3
v C v
v(0) v 0 C 0
v C 0
d’où
x0
y
z
vv
v(t) v g.t
v0
Et
dOM
vdt
donc
x0
y
z
dx
vv
dt
dy
v(t) v g.t
dt
dz
v0
dt
ainsi
01
2
2
z3
x v .t C'
g.t
OM(t) y C'
2
v C'
C’1, C’2 sont des constantes.
Initialement on a
OM(0) OD H.j
donc
1
2
3
x 0 C' 0
OM(0) y 0 C' H
z C' 0
d’où
02
x v .t
g.t
OM(t) y H
2
z0
On isole t =
0
x
v
et on en déduit: y(x) =
2
2
0
g.x
2v
+ H :équation d’une parabole de concavité tournée vers le bas.
Etape 3 Valider.
Il faut d’abord vérifier que La balle passe au-dessus du filet.
En utilisant l’équation de la trajectoire trouvée dans l’étape 2 on calcule y pour x = OF = 12,2m
y =
2
2
9,81 (12,2) 2,20
126
23,6
= 1,60 m > 0,920 m : La balle passe bien au dessus du filet.
avec v0 = 126 km.h-1 = (126 000/3600) m.s-1
La balle frappe le sol en un point B’ (xB’ ; yB’= 0 ).Le service est « mauvais » si xB’ > OB avec OB = L = 18,7 m.
Déterminons xB’ : y(xB’) = 0 soit
2
B'
0
x
g.
2v
+ H = 0 on trouve
2
0
B' 2v .H
xg
en ne gardant que la solution positive.
2
B'
126
2 2,20
3,6
x9,81
= 23,4 m.
Donc xB’ > 18,7 m, le service n’est pas bon…