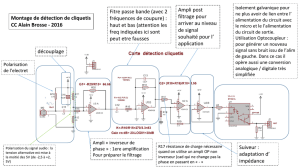
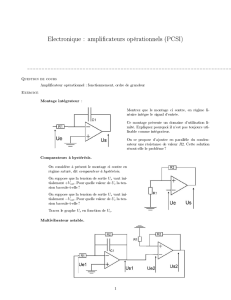
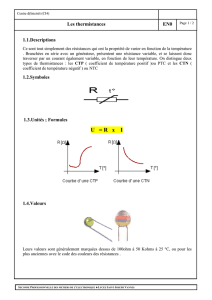
1 Circuits linéaires et ampli cateurs

Rg
UgUL
IL
RLRg
Ig
UL
IL
RL
UL
RL
PL
RL
IL
UL
UL
RL
PL
RL
IL
UL

Ug,k
RkIg,k
Icc Uco
Rthv
Uthv Rnrt
Inrt
UL=Ug
RL
Rg+RL
, IL=Ug
Rg+RL
PL=UL·IL= (Ug)2RL
(Rg+RL)2
RL→0RL→ ∞
RL=Rg
PL, max =(Ug)2
4Rg
=Uco ·Icc
4=Uthv ·Inrt 4

U
U2
R1R2
R2
R1
I
I1I2
U1
Ug,k
RkIg,k U = Σ αk Ug,k + Σ γk Ig,k
[αk] = [V/V], [γk] = [V/A]

Udc
Idc
Ug
Rg
Uin
Iin
UL
IL
RL
Iout
Uout Amplificateur
Source Charge
RL
Au≡Uout
Uin
, Ai≡Iout
Iin
, Ap≡Pout
Pin
Ap≡Pout
Pin
=UoutIout
UinIin
=AuAi
Au,dB ≡20 log (|Au|)Ai,dB ≡20 log (|Ai|)
Ap,dB ≡10 log (Ap) = 10 log (AuAi) = 1
2(Au,dB +Ai,dB)

Uout =Uos +AuUin
Uos Au
Auo ≡∆Uout
∆Uin Iout=0
, Aio ≡∆Iout
∆Iin Uout=0
Rin ≡∆Uin
∆Iin
, Rout ≡∆Uout
−∆Iout Uin=0
A..r
RgRL
Au≡∆Uout
∆Uin RL=···
, Aur ≡∆Uin
∆Uout Ug=0,Rg=···
Rin ≡∆Uin
∆Iin RL=···
, Rout ≡∆Uout
−∆Iout Ug=0, Rg=···
R3
Rin =Uin
Iin
=R1