M1202 TD3 Quantité économique

Département QLIO M1202 Gestion des stocks
Page 1/5 TD 03
TD03 : Quantité économique
Eléments de correction
Exercice 1
La gestion du stock de pièces A suit les règles suivantes :
 On consomme 2000 pièces par an C=2000 unités
 Chaque lancement de commande coûte 22,87 € L=22,87 €
 Le taux de coût de stockage est de 20% Tp=0,2
 Une pièce coûte 1,52 € Cu=1,52 €
Hypothèses :
La consommation de pièces A est constante et régulière.
Une des hypothèses pour permettre l’application de la quantité économique.
Question1
Rappeler les autres hypothèses autorisant l’utilisation de la formule de la quantité
économique.
Calculer la quantité économique d'approvisionnement.
Module 223 : Gestion des Approvisionnements
IUT EVRY Département QLIO 16
CM223 Version 01
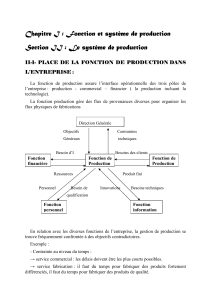
Modèle de base
Q Q Q Q
Stock
moyen
Q/2
Intervalle entre
deux commandes
Niveau
De
stock
Temps
Consommation
Livraison Livraison Livraison
0
Diapositive 16 – Partie 2 du cours
Consommation régulière
et constante ( droite de
pente négative)
Livraison recue en seule
fois (permet de calculer
le stock moyen)
Délai fixe et
connu
Pas de rupture
de stock
Prix unitaire
fixe
Qe=548 unités
CTG=166,76 €

Département QLIO M1202 Gestion des stocks
Page 2/5 TD 03
Question 2
Représenter graphiquement l'évolution des coûts en fonction de la quantité
d'approvisionnement.
Cout de gestion
0
50
100
150
200
250
300
50 100 150 200 250 300 350 400 450 500 550 600 650 700 750 800 850 900 950
Quantité
Coût
CP
CL
CTG
Question 3
Le fournisseur de pièces A, pour des raisons de rentabilité des moyens de transport
impose des lots de 700 pièces. Quelle influence ce changement a-t-il sur le coût global de
gestion de A ?
Par extension, si l'on admet une variation possible du coût global de gestion de A de
+5%, dans quel intervalle la quantité économique d'approvisionnement peut-elle varier ?
Estimer les valeurs de manière graphique et vérifier les valeurs numériques par le calcul.
Première partie :
Si le fournisseur impose des tailles de lots de 700 unités, cela change le coût total de
gestion. Pour Q=700 unités, on trouve CTG=171,74€.
Or pour Qe=548 unités, CTG=166,76€, cela veut donc dire une augmentation de 5€ c’est
à dire 3%. Cela est tout à fait acceptable.
Deuxième partie :
Possible, si le graphique est propre et correctement tracé, de traiter la question de
manière graphique.
Si augmentation de 5%, alors le CTG’=1,05xCTG=1,05x166,76=175,10€

Département QLIO M1202 Gestion des stocks
Page 3/5 TD 03
Cout de gestion
0
50
100
150
200
250
300
50 100 150 200 250 300 350 400 450 500 550 600 650 700 750 800 850 900 950
Quantité
Coût
CP
CL
CTG
De manière graphique, les quantités lues sont 400 et 745 unités.
Par le calcul, il faut résoudre une équation de second degré.
CP+CL=CTG’
1,05xCTGCTG'
Q
CxL
Q
2
CuTp 
Cela donne :
045740175,10,152 QQ2
Nous obtenons après résolution, Q1=400 unités et Q2=752 unités, données proches des
données lues graphiquement.
Conclusion : une faible variation du CTG (5%) permet de choisir une quantité comprise
dans l’intervalle [400 et 752]. La quantité à choisir peut passer du simple au double.
Question 3
Un rabais de 20% sur le prix unitaire des pièces A est consenti pour l’approvisionnement
de toute quantité strictement supérieure à 1000 pièces. Doit-on accepter cette offre ?
Remarque importante : il faut tenir compte ici du coût d’acquisition de pièces.
Sans rabais : coût pour une année pour Qe=548 unités
CL= 83,50 €
CP= 83,30 € CT= 3206,8 €
CA= 3040 €
Avec rabais : coût pour une année pour Q=1000 unités, Cu’=0,8x1,52=1,216 €
Avec un Cu nouveau, il faut calculer Qe’=613 unités (non valable car la remise est valable
pour Q>1000 unités)
CL= 45,7 €
CP= 121,6 € CT= 2599,3 €
CA= 2432 €
Oui, l’offre doit être acceptée car le coût total est plus favorable
pour une quantité de livraison de 1000 unités.
Le bénéfice est de 3206,8 – 2599,3 = 607,5 €.

Département QLIO M1202 Gestion des stocks
Page 4/5 TD 03
Exercice 2
Pour des raisons commerciales, la société GARNIER décide d'adopter le programme de
fabrication suivant , pour trois pièces standard de consommation très régulière :
 3000 unités de P1 par mois
 3000 unités de P2 par mois
 5000 unités de P3 par mois
Les trois produits sont obtenus à partir d'une même matière, chaque produit nécessitant
pour sa fabrication 2 kg de matière.
Pour son approvisionnement, la société Garnier a décidé de passer annuellement un certain
nombre de commandes d'un montant égal. Le coût de passation d'une commande est de
742,50€. Le coût de possession du stock est de 0,36€ par kg et par an.
Pour se prémunir contre les variations possibles de la demande, on crée un stock de
sécurité de 12000 kg de matière.
Hypothèses:
La consommation est constante et une commande est livrée début Janvier.
Question 1
Calculer en fonction du nombre Q de kg contenus dans chaque commande, le coût de
gestion du stock.
C=2x12x(3000+3000+5000)=264000 €
L=742,50 €
CuTp=0,36 € pour 1 kilo
Ss=12000 unités
Q
196020000
0,18xQ
Q
CxL
Q
2
CuTp
CTG 
Question 2
Calculer la quantité économique de commande Qe, le nombre de commandes annuelles Nc,
et la période de réapprovisionnement économique Pe en mois.
CuTp
2xCxL
Qe
Qe=33000 unités
Qe
C
Nc
Nc=8 commandes par an
Nc
12
Pe
Pe=1,5 mois

Département QLIO M1202 Gestion des stocks
Page 5/5 TD 03
Question 3
Soit D le délai (en mois) de réapprovisionnement :
Déterminer pour D = 1 et D = 2 les dates des différentes commandes sur un an.
Nous supposons, au 1er janvier, une quantité en stock de 33000 unités et une aucune
réception est attendue.
Pour D=1 mois : 15-01 / 01-03 / 15-04 / 01-06/ 15-07 / 01-09 / 15-10 / 01-12
Pour D=2 mois : 15-12 / 01-02 / 15-03 / 01-05 / 15-06 / 01-08 / 15-09 / 01-11
Janv.
Fév.
Mars.
Avril.
Mai.
Juin.
Juil.
Aout.
Sept.
Oct.
Nov.
Déc.
Niveau au
stock
D
D
D
D
D
D
D
D
D
D
D
D
D
D
D
D
Janv.
Fév.
Mars.
Avril.
Mai.
Juin.
Juil.
Aout.
Sept.
Oct.
Nov.
Déc.
Niveau au
stock