TD 9 : Réf. non-galiléen - MP

REVITRON.FR
MP-2
TD 9 : Réf. non-galiléen
Exercice 1 D’après ICNA 05, Oral CCP 05
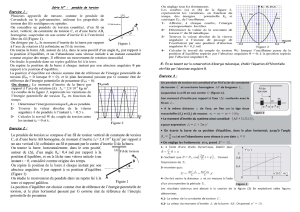
Une perle Pde masse m, considérée ponctuelle, soumise à la pesan-
teur et susceptible de se déplacer sur une tige de longueur 2`tournant
à une vitesse angulaire ~ω autour d’un axe contenant son centre O. L’ac-
célération de la pesanteur ~g est constante et dirigée vers le bas. On note
~r =~ OP le rayon vecteur de la position de Pà l’instant t. Les grandeurs
r0et v0caractérisent la position et la vitesse de la particule à l’instant
t= 0 suivant l’axe Or. La tige est dans le plan horizontal (Ox, Oy) et
tourne autour de l’axe Oz à la vitesse angulaire ω. Les mouvements ont
Figure 1 – Notations.
lieu sans frottement.
1 - Établir l’équation différentielle en rdu mouvement.
2 - Résoudre cette équation pour les conditions initiales r0et v0.
3 - Établir l’expression du temps τque mettra la bille B pour sortir de
la tige, on prendra v0=0m.s−1.
4 - Application numérique : Calculer τpour `= 0,10 m,r0= 0,010 m ;
v0=0m.s−1et ω= 2,0 rad.s−1.
Exercice 2 D’après Oral CCP 11
Un plateau horizontal est en rotation autour de l’axe Ozà la vitesse
angulaire constante ωdans un référentiel Rsupposé galiléen.
Un point matériel Mpeut se déplacer sans frottement sur un rail xx0
infini fixé sur le plateau à une distance dde l’axe Oz. Ce point est soumis
a son poids, à la réaction du support et à une force de rappel ~ F = −k. ~ AM
où Aest le projeté orthogonale de Osur les rail. On notera AM = x.
x
O
ω
z
x’
x
z
x’
O
d
A
M
M
1 - Appliquer le PFD et décrire toutes les forces (norme,direction,sens).
2 - Exprimer l’accélération du point M dans le référentiel du plateau
puis avec la composition des accélérations calculer l’accélération de M
dans R.
3 - Établir l’équation différentielle vérifiée par xet discuter des solu-
tions possibles.
Exercice 3 D’après X 05, Centrale 08
On considère un pendule simple constitué d’une masse Msuspendue
par un fil de longueur L. Le point de suspension O, attaché au sol, est
soumis, par rapport au référentiel RG, galiléen fixe, à un déplacement
horizontal d’origine sismique xO(t). on note RSle référentiel lié au sol.
Figure 2 – Pendule.
1 - Écrire l’équation du mouvement angulaire du pendule dans RS.
La linéariser dans l’hypothèse des petits mouvements angulaires. En
déduire l’équation différentielle reliant le déplacement θ(t)de la masse
Mà celui x0(t)du sol.
MP-2 M. BARTHES

REVITRON.FR
2 - Si x0(t)=X0cos ωt, déterminer l’amplitude des oscillations Θ(ω), où
θ(t) = Θ(ω) cos(ωt +φ).
Exercice 4 D’après "La physique par la pratique"
Dès 1791, Guglielmini réalisa des expériences de chute libre à Bo-
logne pour tester le caractère (non) galiléen du référentiel terrestre.
Une balle de masse métait lancée sans vitesse initiale d’une hauteur
~
OM = h0~ezà la latitude λ= 44,5°. On rappelle que l’attraction terrestre
sur une masse mexerce une force ~ F = −GMTm/r2~ezoù rest la dis-
tance au centre de la Terre. On donne le rayon terrestre : RT= 6400 km,
la masse de la Terre : M=6.1024 kg et la constante de gravitation
G=6,67.10−11 N.m2.kg−2.
Figure 3 – Notations.
1 - Dans le référentiel terrestre tournant à la vitesse angulaire ωet
muni du repère (O, ~ex, ~ey, ~ez), déterminer l’équation différentielle régis-
sant la trajectoire de la balle. On supposera que le référentiel géocen-
trique est galiléen.
2 - En étudiant l’importance des différents termes justifier que
(¨x≈ −2ωcos λ˙z
¨z≈ −GM/R2
T
3 - En posant g= GM/R2
T= 9,8 m.s−2, en déduire que
x=2√2ωcos λh3/2
0
3g1/2
Le déplacement mesuré à Bologne par Guglielmini était de 1,9 cm pour
une hauteur de 78,3 m. Ce résultat vous parait-il cohérent ?
MP-2 M. BARTHES