Feuille d`exercices 9 : corrigé

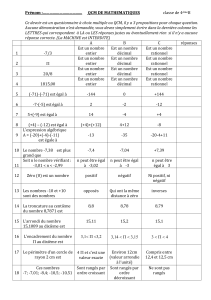
1
7
42
17 =2×3×7 17
2n×5mn m N
27
8=33
23
2n×5mn=3m=0
278=3,375
91 =7×13 91
7=13
1
1,4,2,8,5,7
17
1
7=0,142857.
6 7 6e
12e18e24e30e31e1
32e4
20e42
17 5B22
A18 8 A2
4217
B3B18
42
17 =2,4705882352941176.
17 17 17 0 16
0

42
17 16
1 16 A2
A17 A18
a=1,23 100a=123,23
100a−a=123,23 −1,23 =122,
99a=122
a=122
99 .
p1,117 <p
1789 ⩽1,118
1,117 ×1789 <p⩽1,118 ×1789
1998,313 <p⩽2000,102.
p=1999 p=2000
1999
1789 ≈1,1174 2000 1789 ≈
1,1179
12=36 23=46 12<23
12
13 =12×14 13×14 =168 182
13
14 =13×13 14×13 =169 182
12
13 <13 14
176
177 =176×178 177×178 =31328 31506
177
178 =177×177 178×177 =31329 31506
176
177 <177 178
n−1
n<n n+1⋅
n−1
n=(n−1)×(n+1) n×(n+1)=n2−1 n(n+1)n n+1=n×n (n+1)×n=n2 n(n+1)⋅
n2−1<n2n−1
n<n n+1
n=987 654 322
987 654 321
987 654 322 <987 654 322 987 654 323 ⋅
(OH)(JT )
EJT EO
EJ =OH JT
3r
5r=a ra=3 5r
a=3r
5r a
a=6r
10 a
6r a

a=3r
55 3r
5r5
3r
r a
5 5 10 15
a r =5a=3
OHB
H OB2=OH2+HB2r2=a2+HB2
HB2=r2−a2=r2−3
5r2=r2−9 25 r2=(1−9 25 )r2=16 25 r2.
HB =4
5r
H[AB]OAB O
OA =OB O [AB]
(OH) [AB]
[AB]H[AB]HB
AH
OAH AH =HB H A B
[AB]
b=2HB =8
5r
b=8r
5
5 8r=23×r5r
5 23×r r =5×k
b=8×r
5=8×k b 8
b
a
b
b
a
32
23
a
10na∈Z
n∈N10n
a
32=1,5
23

1
pp+q
2+1
qp+q
2=2
p(p+q)+2 q(p+q)=2q pq(p+q)+2p pq(p+q)
=2p+2q
pq(p+q)=2(p+q) pq(p+q)=2 pq ⋅
p q p +q
2p+q
2
pp+q
2
qp+q
2pq