1. Matrice de transition On place une souris - Loze

1. Matrice de transition
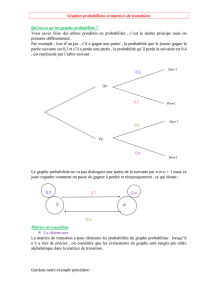
On place une souris dans un compartiment du labyrinthe illustré.
Chaque fois qu’elle entend une sonnerie, apeurée, elle change de
compartiment en choisissant au hasard une des portes du compartiment
où elle se trouve.
Dans le compartiment E, on place un fromage et lorsqu’elle atteint
ce compartiment, la souris n’en bouge plus car, comme chacun sait,
« ventre affamé n’a point d’oreilles »
Déterminer la matrice canonique donnant les probabilités de transition
à partir de chacun des compartiments du labyrinthe.
Solution
On construit la matrice canonique en plaçant les états absorbants dans
le coin supérieur gauche de la matrice. Dans le présent exercice, il y
a un seul état absorbant.
Si la souris est dans le compartiment E, la probabilité qu’elle y reste est
égale à 1 et la probabilité qu’elle aille dans les autres compartiments
est égale à 0.
Si la souris est dans le compartiment A, la probabilité qu’elle aille
dans le compartiment B est de 1/2 et la probabilité qu’elle aille dans
le compartiment D est également de 1/2. On procède de la même
façon si la souris est dans le compartiment B
Si la souris est dans le compartiment C, il y a trois portes et la proba-
bilité de transition vers chacun des compartiments adjacents est 1/3 On
procède de la même façon si la souris est dans le compartiment D.
La probabilité d’aller dans un compartiment non adjacent en une
transition est nulle. En inscrivant ces probabilités dans une matrice,
on obtient :
1 0 0 0 0
0 0 1 2 0 1 2
0 1 2 0 1 2 0
1 3 0 1 3 0 1 3
1 3 1 3 0 1 3 0
Nom :
Groupe :
Algèbre linéaire et géométrie vectorielle | André Ross 1
A
B C
D
E
A
B C
D
E
A
B C
D
E

2 Chapitre 3 | feuille d’exercices
3. Vers un état non absorbant
Calculer la probabilité que la souris n’ait pas trouvé le fromage après
la troisième transition selon le compartiment dans lequel elle est ini-
tialement placée.
Solution
Pour déterminer la probabilité que la souris n’ait pas trouvé le fromage
après la troisième transition, il faut calculer le cube de la matrice Q
du coin inférieur droit de la matrice canonique*.
Q=
0 1 2 0 1 2
1 2 0 1 2 0
0 1 3 0 1 3
1 3 0 1 3 0
Q2
0 1 2 0 1 2
1 2 0 1 2 0
0 1 3 0 1 3
1 3 0 1 3 0
0 1 2 0 1
= •
22
1 2 0 1 2 0
0 1 3 0 1 3
1 3 0 1 3 0
5 12 0 5 12 0
0 5 12
=00 5 12
5 18 0 5 18 0
0 5 18 0 5 18
Note :
Rappelons d’abord qu’en élevant une matrice canonique à une puissance n, les
sous matrices se combinent entre elles en préservant la forme canonique.
Ainsi, en élevant une matrice P sous forme canonique à la puissance 3, on a dans
le coin supérieur gauche, la sous matrice identité d’ordre r, où r est le nombre
d’états absorbants. Dans le coin supérieur droit, on a la matrice nulle de dimen-
sion r × s où r + s est le nombre d’états de la chaîne de Markov.
P=Ir×rOr×s
Rs×rQs×s
 et P3=Ir×rOr×s
(R+Q•R+Q2•R)s×rQs×s
3
Probabilité que la souris
ait trouvé le fromage après
trois changements de cellule.
Probabilité que la souris
n’ait pas trouvé le fromage après
trois changements de cellule.
Dans le coin inférieur gauche, on a les probabilités que le système soit dans un
état absorbant après trois transitions et dans le coin inférieur droit, la probabilité
que le système soit dans un état non absorbant après trois transitions. En pratique,
on effectue simplement les opérations sur les sous matrices R et Q.

Algèbre linéaire et géométrie vectorielle | André Ross 3
Q3
0 1 2 0 1 2
1 2 0 1 2 0
0 1 3 0 1 3
1 3 0 1 3 0
5 12 0 5
= •
112 0
0 5 12 0 5 12
5 18 0 5 18 0
0 5 18 0 5 18
0 25 7
=
22 0 25 72
25 72 0 25 72 0
0 25 108 0 25 108
25 108 0 25 108 0
La matrice Q3 indique que si la souris était initialement dans le com-
partiment A, la probabilité qu’elle soit dans le compartiment B après
trois transitions est de 25 chances sur 72.
Initialement en A
A
B
B
C
C
D
D
0 25 72 0 25 72
25 72 0 25 72 0
0 25 108 0 25 108
25 108 0 25 108 0
La probabilité qu’elle soit dans le compartiment D après trois transi-
tions est également de 25 chances sur 72.
Il est impossible qu’après la troisième transition elle soit dans le
compartiment A ou dans le compartiment C. On peut faire la même
analyse pour chaque compartiment.
En multipliant la matrice Q3 par la matrice de dimension 4 par 1 dont
tous les éléments sont des uns, on fait la somme des éléments sur
chacune des lignes.
0 25 72 0 25 72
25 72 0 25 72 0
0 25 108 0 25 108
25 108 0 25 108 0
=•
1
1
1
1
50 72
50 72
50 108
50 1088
25 36
25 36
25 54
25 54
=
Au total, la probabilité que la souris n’ait pas trouvé le fromage si
elle était initialement dans le compartiment A est de 50 chances sur
72 ou de 25 chances sur 36.
A
Probabilités de ne pas
avoir trouvé le fomage
après trois changements
de cellule selon
la cellule initiale.
B
C
D
25 36
25 36
25 54
25 54

4 Chapitre 3 | feuille d’exercices
2. Vers un état absorbant
Calculer la probabilité que la souris ait trouvé le fromage après la
troisième transition selon le compartiment dans lequel elle est initia-
lement placée.
Solution
En calculant la sous matrice du coin inférieur gauche de la matrice P3,
on détermine la probabilité que la souris ait trouvé le fromage selon
le compartiment où elle est placée initialement.
Cette sous matrice est R + Q•R + Q2•R.
Q R• •=
0 1 2 0 1 2
1 2 0 1 2 0
0 1 3 0 1 3
1 3 0 1 3 0
0
0
1 3
11 3
Q R
2
5 12 0 5 12 0
0 5 12 0 5 12
5 18 0 5 18 0
0 5 18 0 5 18
•= •
0
0
1 3
1 3
R Q R Q R+ + = + • •
2
0
0
1 3
1 3
1 6
1 6
1 9
1 9
+ =
5 36
5 36
5 54
5 54
11 36
11 36
29 544
29 54
La somme des matrices de probabilités indique que si la souris était
initialement dans le compartiment A, la probabilité qu’elle trouve le
fromage après la troisième transition est de 11 chances sur 36. On
fait une analyse analogue pour les autres compartiments.
On peut reconstituer la matrice P au cube en insérant les résultats
des calculs sur les sous matrices. On remarque que la matrice P au
cube est une matrice de transition puisque la somme des éléments de
chacune des lignes est égale à 1.
Probabilités d’avoir
trouvé le fromage
après trois changements
de cellule selon
la cellule initiale.
A
B
C
D
11 36
11 36
29 54
29 54
Après trois changements
de cellule selon
la cellule initiale.
A
+=
B
C
D
25 36
25 36
25 54
25 54
1
1
1
1
11 36
11 36
29 54
29 54
Pas trouvé SommeTrouvé
A
A
E
E
Probabilités d’état
après trois transitions
B
B
C
C
D
D
1 0 0 0 0
11 36 0 25 72 0 25 72
11 36 25 72 0 25 72 0
29 54 0 25 108 0 25 108
29 54 25 108 0 25 108 0